数据结构:红黑树的删除(进击的Java新人Week.6学习笔记)

Posted on |

Author: Kelvin

注意： 由于红黑树删除相对复杂，看到另一篇博客写的非常好，故本文内容基本来自红黑树删除，代码自己实现)

一、节点命名约定

 D表示要被删除的节点。即：取 Delete 的首字母
 P 表示父节点。即：取 Parent 的首字母
 S表示兄弟姐妹节点。即：取  Sibling的首字母
 U表示叔伯节点。即：取Uncle的首字母
 G表示祖父节点。即：取  Grandfather的首字母
 L表示左树。即：取Left的首字母
 R表示右树。即：取Right的首字母
 Nil表示叶子节点。即所谓的空节点；注意：红黑树中的叶子节点与其他树中所述说的叶子节点不是同一概念。而且红黑树中的叶子节点(即：Nil节点)永远是被定义为黑色的

下文的节点命名表示将会使用以上这些命名约定或它们的组合表示。因此，请先牢记这些命名约定。举例
DR表示要被删除的节点的右子树，即：右子节点；
SL表示兄弟节点的左子树，即：左子节点；
…

二、删除操作宏观分析

在红黑树中，删除一个节点往大的说，只有以下四种情况。

情况一：删除的节点的左、右子树都非空；
情况二：删除的节点的左子树为空树，右子树非空；
情况三：删除的节点的右子树为空树，左子树非空；
情况四：删除的节点的左、右子树都为空树；

其中情况一，可以按与其他二叉搜索树的删除方式一样处理，最终可以转换到后面的三种情况。具体为：找到(Old)D节点的直接后继节点(暂且称为X节点)，然后将X的值转移到D节点，最后将X节点作为真正要被删除掉的节点(即：(Real)D节点)。这样删除操作后，可以保证该树仍然为一棵二叉搜索树。但由于红黑树的定义(即：红黑树的性质)约定。这样删除(Real)D节点后，可能会破坏红黑树的性质。所以需要额外做一些调整处理，这便是下面将要详细讨论的内容。

说明：下文中所提到的D，除非有特别说明，否则都将指的是(Real)D。

三、红黑树删除后平衡处理

在具体分析之前，再次列出红黑树的定义：
  (1) 每个节点或者是红色，或者是黑色
  (2) 根节点一定是黑色
  (3) 所有叶子节点都是黑色的。【红黑树中的叶子节点也叫NIL节点，是指空的叶子节点】
  (4) 如果一个节点是红色的，则它的子节点必须是黑色的。（任何两个父子节点不可能同时为红色）
  (5) 任意节点到其所有分支叶子节点的简单路径上的黑色节点个数相同。（该属性保证红黑树始终是一颗接近平衡的二叉树）
下面是几个图示说明：
01
根据红黑树的定义，被删除的节点D(即：上文所述的(Real)D节点)不论如何都一定有一个“右子树”，只是该右子树要不为非空树(即：真正存在的节点，不为Nil节点)，要不就必为空树(即：D的两个子节点都为Nil)。下面称D的该右子节点(或称为右子树)为DR。

a) 被删除的D节点为红色。这种情况，则与D相关的颜色以及结构关系必然只有如下一种情况(为什么只有这种情况，不明白的请看红黑树的性质)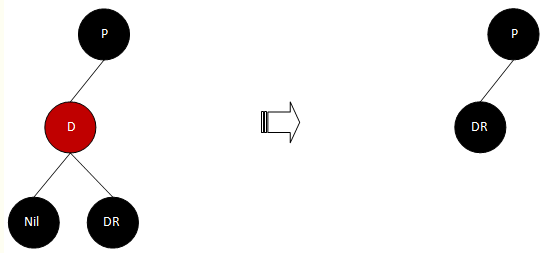：02
分析：因为D为红色，所以P必为黑色，同时DR不可能为红色(否则违反性质4)。同时由于性质5，则DR必为Nil，否则就D树来说，经过DR与不经过DR的路径的黑节点数必不相同。现在要删除D节点，只需要直接将D节点删除，并将DR作为P的左子节点即可。因此删除后，变成上图右侧所示。

b) 被删除的D节点为黑色。此时情况会稍复杂些，具体又分析为：DR为Nil与DR不为Nil。根据性质5，如果DR不为Nil，则DR必为红色，且DR的两个子节点必为Nil。因此，此处先来分析DR不为Nil的情况(因为该情况比较简单)。而DR为Nil的情况，由后面的C)及其后内容再进行具体分析 。
如前所述，如果DR不为Nil，则D、DR必为如下情况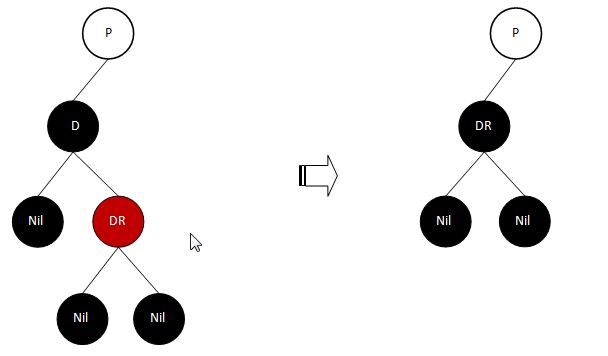：03
分析：由于删除的D为黑色，删除后P的左子树的黑节点数必少1，此时刚好DR为黑色，并且删除后DR可以占据D的位置(这样仍是一棵二叉搜索树，只是暂时还不是合格的红黑树罢了)，然后再将DR的颜色改为黑色，刚好可以填补P左子树所减少的黑节点数。从而P树又平衡了。因此，平衡处理后，最终变成上图右侧的图示。

c) 被删除的D为黑色，且DR为Nil。
如果DR为Nil，则删除D后，P的左子树黑节点数必定少1，纯粹想在P的左子树做文章来平衡P树是绝无可能的了。因此，必定需要其他分支的辅助来最终完成平衡调整。根据红黑树的定义，P会有一个右子节点，称为S子节点。此处又可细节分两种情况：黑S与红S。此处先讨论红S的情况。

说明：如果S为黑，则它必不会为Nil。(不明白的人，再好好想想为什么)。同时根据红黑树的性质，D、S、P、SL、SL的颜色关系必只有如下一种情况(因为此处探讨的是S为红的情况)。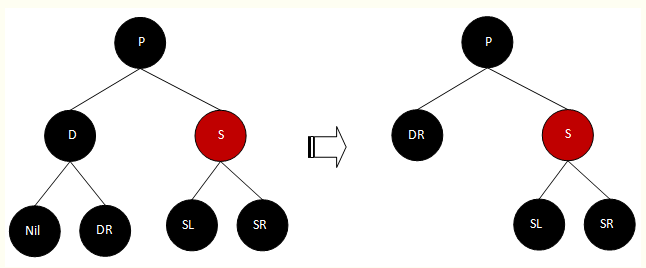
04
分析：删除前P树的左、右子树的黑节点数平衡，删除后(即：上图右侧所示)，经过DR分支的黑节点数将比通过S分支的黑节点数少1。此时，做如下操作
将P左旋转，再将P由黑色改为红色，将S由红色改为黑色，演变过程如下图示：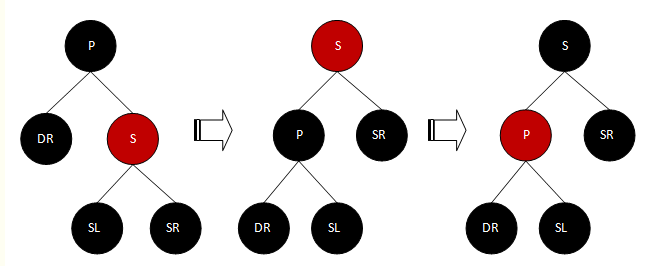
05
经过以上演变后，经过P的路径，左分支黑节点数仍是少1，其他分支的黑节点数做仍然保持不变。此时的情况却变成DR的兄弟节点为黑色(不再是红色的情况了)，因此转入此处c)点一开始所说的另一种情况(S为黑色的情况)的处理。

注意：可能有人会一时想不明白什么要这样转换。因为这样转换后，虽然对于P树的左子树的黑节点数仍然会比右子树的黑节点数少1，但此时DR的兄弟(以前的S节点)现在已经变为SL，即已经由红色变为黑色，并且非常重要的此时的DR的兄弟节点SL的子结点(即：DR的两个侄子节点)，要不就是红色节点要不就必为Nil节点，而这种情况正是D为黑色、S也黑色的情况。(注意看注意看注意看一定注意看这点：对于被删除节点D的父节点来说，D黑S黑的情况下，无论如何D的兄弟节点S的两个儿子节点SL与SR都不可能是非Nil的黑节点。不明白的好好想想为什么)。因此我们有了进一步分析的余地。

d) 被删除的D为黑色，S也为黑色的情况。根据D、P、S、SL、SR的颜色组合情况，本来是有非常多种变换的。但事实上，我们只需要按如下4种情况做进一步的处理，即可全部涵盖所有的颜色组合情况。
d.1> SL为红，SR颜色任意；(对于该情况的处理，其实我们不关心P的颜色)
d.2> SR为红，SL颜色任意；(对于该情况的处理，其实我们不关心P的颜色)
d.3> SL、SR都为黑；P为红。(注意：根据前面c)点的红色文字部分的分析，此时SL与SR必定必定都为Nil节点)；
d.4> SL、SR都为黑；P为黑。(注意：根据前面c)点的红色文字部分的分析，此时SL与SR必定必定都为Nil节点)；

d.1> SL为红，SR颜色任意情况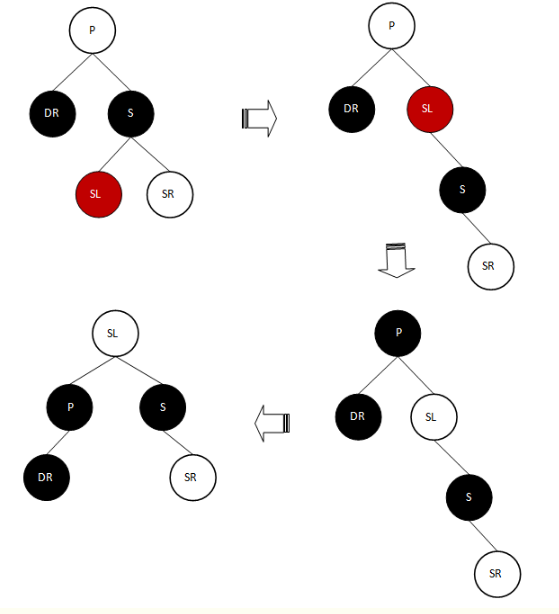
06
分析：P树的左子树黑节点数减少1，因此，要想平衡，必需想办法让左子树的黑结节数增加1，而且同时P的右子树的黑节点数要保持不变。因此，想办法将SL这个红色节点利用起来，让它来填补P的左子树所缺少的黑节点个数。因此，立马想到旋转，只要有办法转到P的左子树或P位置上，则就有可能填平P左子树的高度。所以具体操作步骤为：
将S右旋转；接着将SL改为P的颜色，P的颜色改为黑色(用这个黑色来填补DR分支的黑节点数)；将P左旋转。

d.2> SR为红色，SL颜色任意的情况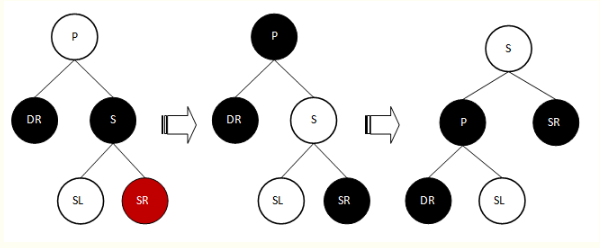
07
分析：思路同d.1>情况类似，都是想办法用红色的SR节点来填补P的左子树的减少的黑节点数。具体步骤为：
将S由黑色改为P的颜色；
将SR由红色改为黑色；
将P的颜色改为黑色(用该黑色来填补DR分支缺失的黑节点数)；
将P节点左旋转；

d.3> SL、SR都为黑色(其实都为Nil节点)，P为红色的情况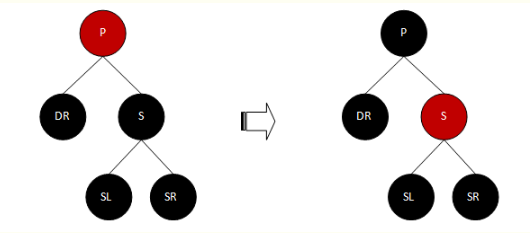
08
分析：此情况较为简单，直接将红色的P改为黑色，以此为填补DR缺少的黑节点个数。此时P右子树黑节点数却增多，因此，再将S改为红色即可平衡。

d.4> SL、SR都为黑色(其实都为Nil节点)，P为黑色的情况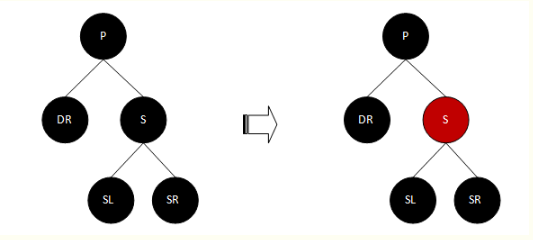
09
分析：因为DR、P、S、SL、SR全都为黑色，则不论如何变换，都永远不可能使用P的左右子树的黑节点数达到平衡。而P不平衡的原因是因为P的右子树黑节点数会比左子树多1个。因此，干脆将S由黑色改为红色，如此一来，P的左、右子树的黑节点个数是平衡的。但是，此时经过P的路径的黑节点个数将会比不经过它的路径少一个。因此，我们将P作为待平衡的节点(即：此时的P相当于DR的角色)往上继续上溯，直到P为根节点为止。

四、红黑树删除代码实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
//删除节点
	public void remove(T key){
		RBTNode<T> node = search(this.mRoot, key);
		if(null!=node){
			remove(node);
		}
	}
	
	private void remove(RBTNode<T> node) {
		RBTNode<T> child=null,parent=null;
		boolean color=false;
		
		//删除的节点有两个孩子,转化为删除该节点的后继节点
		if((node.left!=null) && (node.right!=null)){
			//记录后继节点
			RBTNode<T> replace = node.right;
			while(replace.left!=null)
				replace = replace.left;
			
			child = replace.right;
			parent = replace.parent;
			if(parent==node){
				node.right = child;
				if(child!=null){
					child.parent = node;
				}
			}else {
				parent.left = child;
				if(child!=null){
					child.parent = parent;
				}
			}
				
			//将后继节点数据拷贝到待删除节点
			node.key = replace.key;	
			color = replace.color;
			if(color==BLACK){
				removeFixUp(child,parent);
			}
			replace = null;
			return;
		}
		
		if(node.left!=null){
			child = node.left;
		}else {
			child = node.right;
		}
		parent = node.parent;
		
		if(parent!=null){
			if(parent.left==node){
				parent.left = child;
			}else {
				parent.right = child;
			}
		}else {
			this.mRoot = child;
		}
		
		if(child!=null){
			child.parent = parent;
		}
		if(node.color==BLACK){
			removeFixUp(child,parent);
		}
		node = null;
	}

	//删除节点后，修正红黑树
	private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
		//node的兄弟节点
		RBTNode<T> silNode = null;
		
		//如果node是黑色的话，那么必为NIL节点
		while((node == null || isBlack(node)) && (node != this.mRoot)){
			if (parent.left == node) {
				silNode = parent.right;
				if(isRed(silNode)){		//case 1: 兄弟节点是红色节点，则parent为黑色，silNode的两个儿子都为黑色
					setBlack(silNode);
					setRed(parent );
					leftRotate(parent);
					silNode = parent.right;
				}

				//case 2: 兄弟节点是黑色节点,其左右孩子都为黑色
				if((silNode.left==null || isBlack(silNode.left) && (silNode.right==null || isBlack(silNode.right)))){
					setRed(silNode);
					node = parent;
					parent = parentOf(node);
					continue;
				}else {
					//case 3: 兄弟节点是黑色，左孩子是红色，右孩子是黑色
					if(silNode.right==null || isBlack(silNode.right)){
						if(silNode.left!=null)
							setBlack(silNode.left);
						setRed(silNode);
						rightRotate(silNode);
						silNode = parent.right;
					}

					//case 4: 兄弟节点黑色，左孩子任意颜色，右孩子是红色
					silNode.color = parent.color;
					setBlack(parent);
					if(silNode.right!=null){
						setBlack(silNode.right);
					}
					leftRotate(parent);
					break;
				}
			}else {
				silNode = parent.left;
				if(isRed(silNode)){
					setBlack(silNode);
					setRed(parent );
					rightRotate(parent);
					silNode = parent.left;
				}

				if((silNode.left==null || isBlack(silNode.left) && (silNode.right==null || isBlack(silNode.right)))){
					setRed(silNode);
					node = parent;
					parent = parentOf(node);
					continue;
				}else {
					//case 3: 兄弟节点是黑色，左孩子是黑色，右孩子是红色
					if(silNode.left==null || isBlack(silNode.left)){
						if(silNode.right!=null)
							setBlack(silNode.right);
						setRed(silNode);
						leftRotate(silNode);
						silNode = parent.left;
					}

					//case 4: 兄弟节点黑色，右孩子任意颜色，左孩子是红色
					silNode.color = parent.color;
					setBlack(parent);
					if(silNode.left!=null){
						setBlack(silNode.left);
					}
					rightRotate(parent);
					break;
				}
			}
		}
		
		//如果node不是NIL节点，则必为红色
		if(node != null)
			setBlack(node);
	}

了解红黑树及所有代码实现，请看另一篇博客 红黑树