Author: Kelvin
一、红黑树介绍
红黑树(Red-Black Tree, 简称RBTee),是一种特殊的二叉查找树。它满足二叉查找树的特征: 任意一个节点所包含的键值,大于左孩子的键值,小于等于右孩子的键值。
顾名思义,红黑树的每个节点上具有一个表示颜色的属性,红色或者黑色。
- 红黑树的节点定义
1 | public class RBTNode<T extends Comparable<T>> { |
- 红黑树的特征
必须满足以下特征的二叉查找树才是红黑树。
(1) 每个节点或者是红色,或者是黑色
(2) 根节点一定是黑色
(3) 所有叶子节点都是黑色的。【红黑树中的叶子节点也叫NIL节点,是指空的叶子节点】
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。(任何两个父子节点不可能同时为红色)
(5) 任意节点到其所有分支叶子节点的简单路径上的黑色节点个数相同。(该属性保证红黑树始终是一颗接近平衡的二叉树)
二、红黑树的基本操作(左旋和右旋)
- 左旋
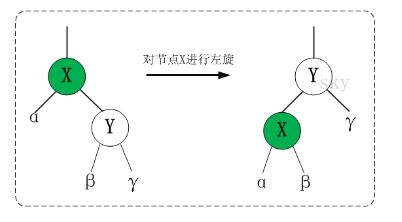
代码实现:
1 | /* |
- 右旋
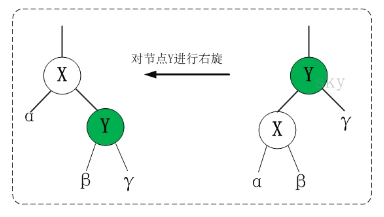
代码实现:
1 | /* |
三、添加节点
我们知道,一棵树之所以成为红黑树,必须要满足红黑树的五个特征。对红黑树的插入操作,必然有可能会影响红黑树特性,因此我们需要对其进行修正。红黑树的插入主要分为三个步骤:
1. 将红黑树当作一颗二叉查找树,将节点插入
2.将插入的节点着色为”红色”
3.通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
- 插入节点后,对红黑树的影响分析
新插入的节点,默认是红色(因为如果是黑色,就会直接影响红黑树的特性5,调整很麻烦);我们设置新插入的节点为N,其父节点为P,其祖父节点为G,其父亲P的兄弟节点为U。当父节点P是黑色的,不需要调整,下面主要讨论P是红色的情况。
- 当U是红色的。将P和U重绘为黑色并重绘结点G为红色。现在新结点N有 了一个黑色的父结点P,因为通过父结点P或叔父结点U的任何路径都必定通过祖父结点G, 在这些路径上的黑结点数目没有改变。但是,红色的祖父结点G的父结点也有可能是红色 的,这就违反了性质3。为了解决这个问题,我们在祖父结点G递归向上调整颜色
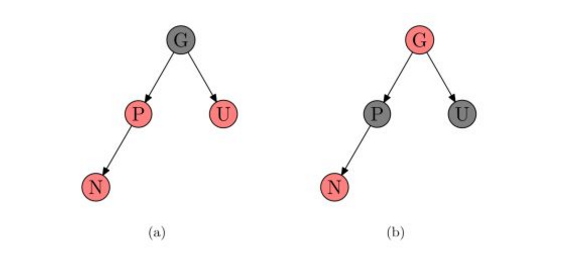
- 当U是黑色,且N是左孩子。对祖父结点G 的一次右旋转; 在旋转产生的树中,以前的父结点P现在是新结点N和以前的祖父节点 G 的父结点,然后交换以前的父结点P和祖父结点G的颜色,结果仍满足红黑树性质
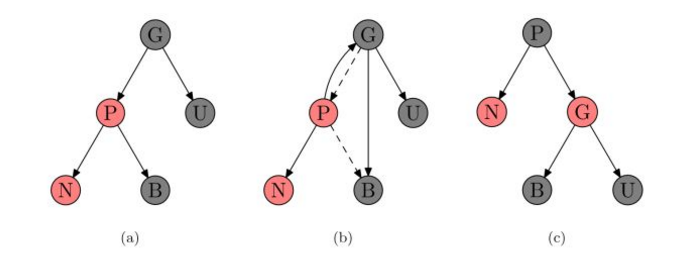
- 当U时黑色,且N是右孩子。我们对P进行一次左旋转调换新结点和其父 结点的角色,就把问题转化成了第二种情况,此时对G做一次有旋转即可。
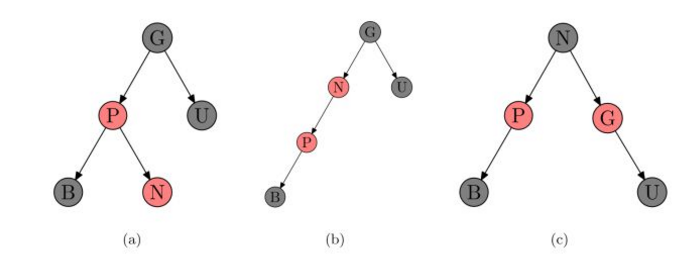
以上所分析的是当P是左孩子时的情况,当P时右孩子的情况跟是左孩子的情况一样,旋转的方向不一样而已,请读者自行分析。
- 红黑树的插入代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119//添加节点
public void insert(T key){
if(null==key){
return;
}
this.insert(new RBTNode<T>(BLACK, key));
}
private void insert(RBTNode<T> node){
if(this.mRoot==null){
this.mRoot = node;
return;
}
RBTNode<T> curr = this.mRoot;
int rs = 0;
while(true){
rs = node.key.compareTo(curr.key);
if(rs < 0){
if(curr.left != null){
curr = curr.left;
}else {
curr.left = node;
node.parent = curr;
break;
}
}else {
if(curr.right != null){
curr = curr.right;
}else {
curr.right = node;
node.parent = curr;
break;
}
}
}
node.color = RED;
//由于新插入节点会影响红黑树的结构,需要修正使其满足红黑树的性质
insertFixUp(node);
}
//插入节点后修正红黑树
private void insertFixUp(RBTNode<T> node) {
RBTNode<T> parent, gparent;
parent = parentOf(node);
//若父节点存在,且父节点的颜色是红色
while((parent = parentOf(node))!=null && isRed(parent)){
gparent = parentOf(parent);
if(gparent==null){
break;
}
//若父节点是祖父节点的左孩子
if(parent == gparent.left){
//叔叔节点
RBTNode<T> uncle = gparent.right;
// case 1: 叔叔节点是红色
if(uncle!=null && isRed(uncle)){
setBlack(uncle);
setBlack(parent);
if(gparent != this.mRoot){
setRed(gparent);
}
node = gparent;
continue;
}
//case 2: 叔叔是黑色,当前节点是右孩子或者叔叔是null
else if(parent.right==node){
leftRotate(parent);
setBlack(node);
if(gparent != this.mRoot){
setRed(gparent);
}
rightRotate(gparent);
node = parent;
}
//case 3: 叔叔是黑色,当前节点是左孩子或者叔叔是null
else{
setBlack(parent);
if(gparent != this.mRoot){
setRed(gparent);
}
rightRotate(gparent);
}
}else { //父节点是祖父节点的右孩子
RBTNode<T> uncle = gparent.left;
// case 4: 叔叔节点是红色
if(uncle!=null && isRed(uncle)){
setBlack(uncle);
setBlack(parent);
if(gparent != this.mRoot){
setRed(gparent);
}
node = gparent;
continue;
}
//case 5:叔叔节点是黑色,且当前节点是左孩子或者叔叔是null
else if(parent.left == node){
rightRotate(parent);
setBlack(node);
if(gparent != this.mRoot){
setRed(gparent);
}
leftRotate(gparent);
node = parent;
}
else {//case 6:叔叔节点是黑色,且当前节点是右孩子或者叔叔是null
setBlack(parent);
if(gparent != this.mRoot){
setRed(gparent);
}
leftRotate(gparent);
}
}
}
}
四、删除节点
由于红黑树的删除较复杂,请看另一篇博客 红黑树的删除
五、红黑树代码实现
1 | package cn.kelvin.oocl.rbtree; |