Author: Yellow
进击的Java新人Week.1学习笔记
Week.1的课程主要包括以下几部分:
- 有符号整数在计算机中的表示、不同进制之间的转换;
- Java中
static、final关键字; - Java中自动装箱拆箱的坑
有符号整数在计算机中的表示、不同进制之间的转换
1. 原码、反码与补码
对于有符号(sign)整数来说,由于其最高位要用来表示符号 (0 = 非负,1 = 负),所以其能表示的数的最大绝对值要比无符号数小一半。已Java中的byte来作为例子,由于其长度为8bit,所以其表示范围为-128~127(即-2^7 ~ 2^7-1,为什么右边要减一?因为“0”占了一个位置啊)。
对于正数来说,它的原码、反码、补码都等于其二进制形式。
对于负数来说,它的原码、反码、补码是不同的:
- 原码:把符号位设为1,后面的数字等于这个负数的绝对值,例如-15就变成了10001111。
- 反码:在原码的基础上,保持符号位不变,后面的数字全部取反,例如-15就变成了11110000。
- 补码:它是由反码加1得到的。例如,-1的反码是11111110,再加1就是11111111。
使用补码的好处包括,0和-0的表示是相同的,正负数可以直接进行加减法运算,不必再做额外的转换。而原码和反码则不具备这样的优点。所以现代计算机都是使用补码来表示负数。
2. 不同进制之间的转换
首先,十进制和二进制的互换是最简单的。基本上十进制 -> 二进制就是通过除法求余数: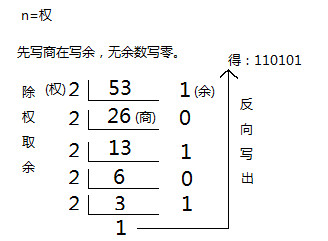
二进制 -> 十进制则是通过乘法: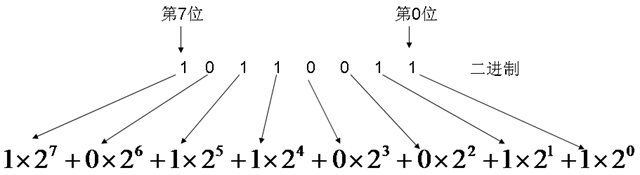
对于任意进制之间的转换,基本就是先转成10进制, 再由10进制转换成目标进制的方法。
3. Java中数值类型的隐式转换
平时写程序时,如果二元运算符两边都是数字,则要特别注意其中隐式转换的坑:
- Byte.MAX_VALUE + 1 会隐式向上转型成int(字面量“1”被认为是int)
- 向上提升时会保持符号位
- 向下转型时会丢失精度或符号位
- byte -> short,char → int → long → float → double(从左往右精度不断上升)
- boolean不能转换成数值
4. “老鼠喝毒药”的解法
没看过题目的可以先看题目。
本质上是用每一只老鼠表示二进制的每一个bit, 则10只老鼠能组合成2^10=1024种组合.
则1000杯水可以按序号用二进制编码:
第1杯 -> 00000 00001
第2杯 -> 00000 00010
第3杯 -> 00000 00011
….
然后第n杯酒就让二进制bit为1的老鼠喝, 看看谁挂掉, 由挂掉老鼠的bit就知道是对应哪杯水