Author: Harry He

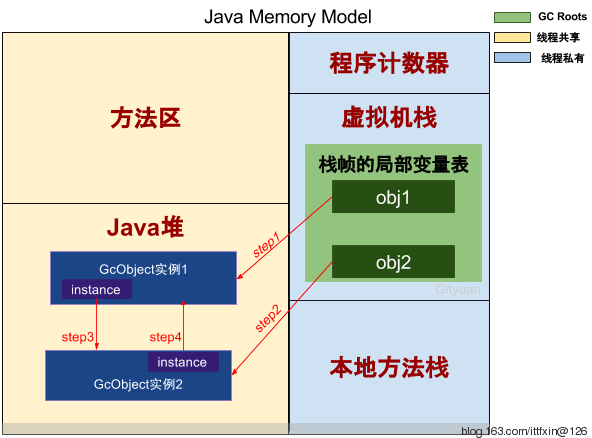
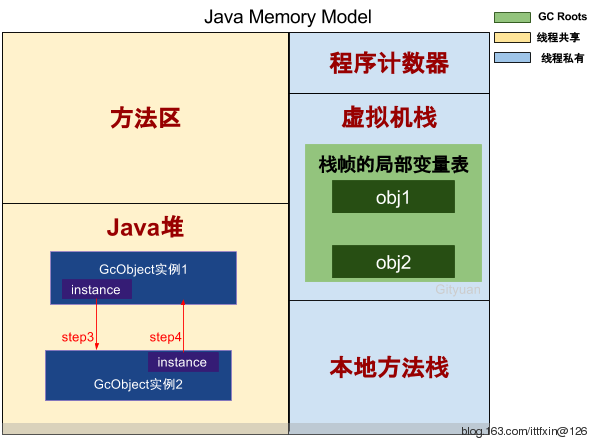
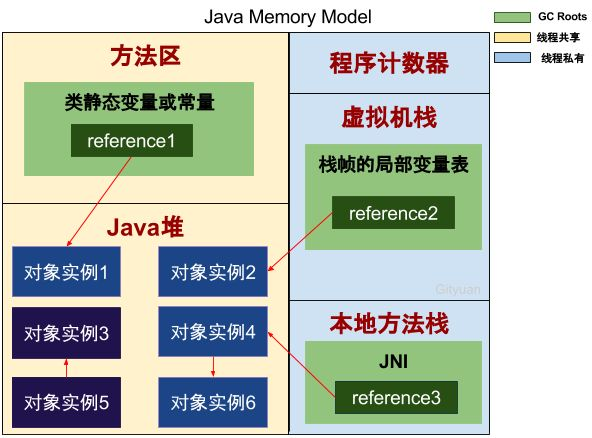
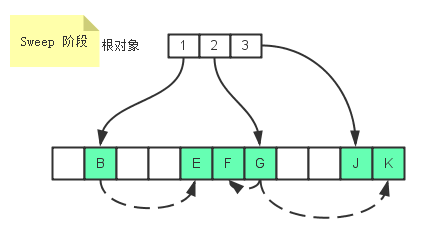
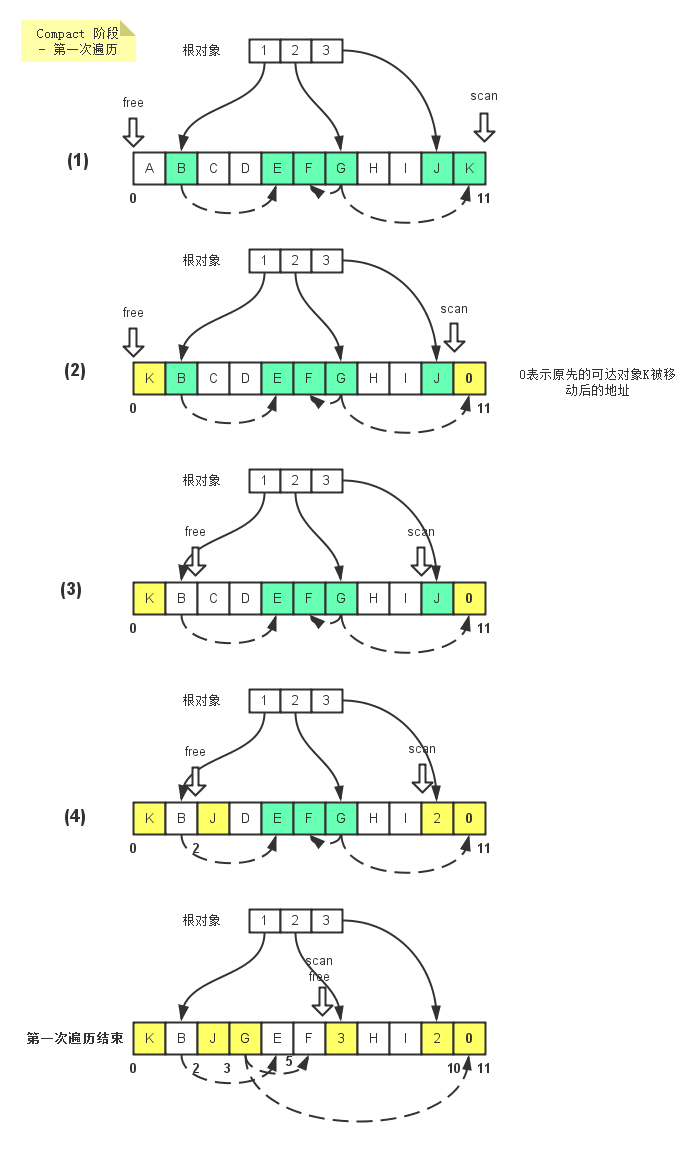
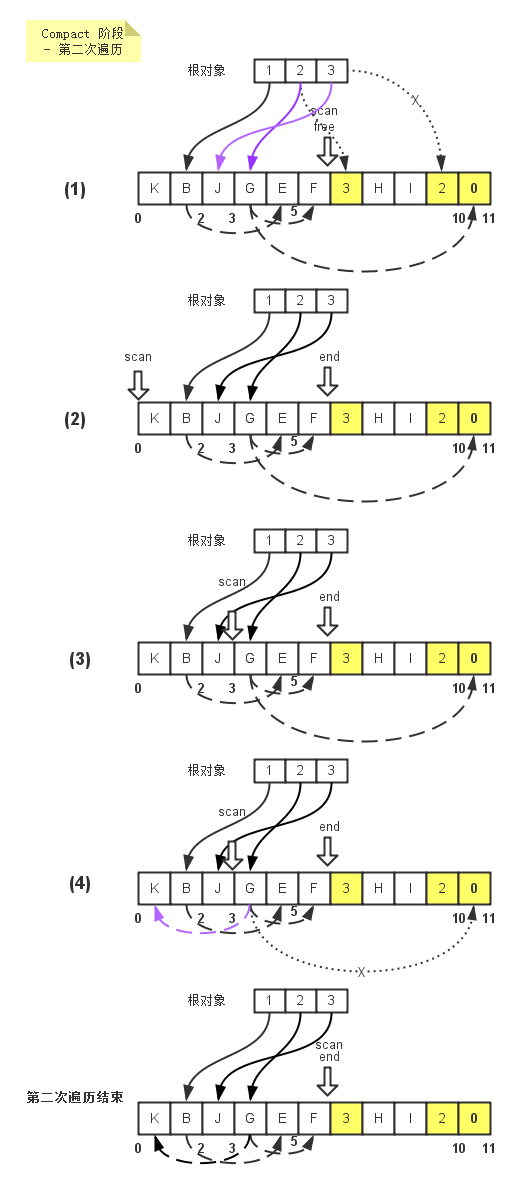
在Java里, 当一个对象o被创建时, 它被放在Heap里. 当GC运行的时候, 如果发现没有任何引用指向o, o就会被回收以腾出内存空间. 或者换句话说, 一个对象被回收, 必须满足两个条件: ==1)没有任何引用指向它 2)GC被运行==.
在现实情况写代码的时候, 我们往往通过把所有指向某个对象的==referece置空==来保证这个对象在下次GC运行的时候被回收 (可以用java -verbose:gc来观察gc的行为)

1
2

Object c = new Car();
c=null;

对于简单的情况, 手动置空是不需要程序员来做的, 因为在java中, 对于简单对象, 当调用它的方法执行完毕后, 指向它的引用会被从stack中popup, 所以他就能在下一次GC执行时被回收了.

但是也有例外，当使用==cache==的时候, 由于cache的对象正是程序运行需要的, 那么只要程序正在运行, cache中的引用就不会被GC给(或者说, cache中的reference拥有了和主程序一样的life cycle). 那么随着cache中的reference越来越多, GC无法回收的object也越来越多, 无法被自动回收. 当这些object需要被回收时, 回收这些object的任务只有交给程序编写者了. 然而这却违背了GC的本质(自动回收可以回收的objects).

==所以就引入了weak reference==

1

Object c = new Car(); //只要c还指向car object, car object就不会被回收

1

WeakReference<Car> weakCar = new WeakReference(Car)(car);

当要获得weak reference引用的object时, 首先需要判断它是否已经被回收: ==weakCar.get();==

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

public class Car {
	private double price;
	private String colour;
	
	public Car(double price, String colour){
		this.price = price;
		this.colour = colour;
	}
	
	public double getPrice() {
		return price;
	}
	public void setPrice(double price) {
		this.price = price;
	}
	public String getColour() {
		return colour;
	}
	public void setColour(String colour) {
		this.colour = colour;
	}
	
	public String toString(){
		return colour +"car costs $"+price;
	}
	
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import java.lang.ref.WeakReference;

public class TestWeakReference {

	
	public static void main(String[] args) {
		
		Car car = new Car(22000,"silver");
		WeakReference<Car> weakCar = new WeakReference<Car>(car);
		int i=0;
		while(true){
			if(weakCar.get()!=null){
				i++;
				System.out.println("Object is alive for "+i+" loops - "+weakCar);
			}else{
				System.out.println("Object has been collected.");
				break;
			}
		}
	}

}

程序运行一段时间后, 程序打印出”==Object has been collected==.” 说明, weak reference指向的对象的被回收了.

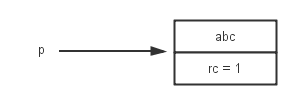
WeakReference的一个特点==是它何时被回收是不可确定的, 因为这是由GC运行的不确定性所确定的==. 所以, 一般用weak reference引用的对象是有价值被cache, 而且很容易被重新被构建, 且很消耗内存的对象.

ReferenceQueue

在weak reference指向的对象被回收后, weak reference本身其实也就没有用了. java提供了一个ReferenceQueue来保存这些所指向的对象已经被回收的reference. 用法是在定义WeakReference的时候将一个ReferenceQueue的对象作为参数传入构造函数.

1
2
3
4

Reference(T referent, ReferenceQueue<? super T> queue) {
       this.referent = referent;
       this.queue = (queue == null) ? ReferenceQueue.NULL : queue;
   }

Author: Harry He

Serial 收集器

单线程收集器，收集垃圾时候必须暂停所有的工作线程，直到它收集结束。

用途：依然是虚拟机运行在客户端模式下的默认新生代收集器

特点：简单高效（与其他收集器的单线程相比），对于限定单个CPU的环境来说，它没有线程交互的开销。
在用户的桌面应用场景中分配给虚拟机管理的内存一般来说不会很大，收集几十兆甚至一两百兆的新生代，停顿的时间完全可以控制在几十毫秒到一百多毫秒以内，只要不平凡发生，还是可以接受这点停顿的。

（老年代和新生代也是和内存相关，虚拟机初始化时已经设定了使用的内存大小，并划分为三部分：新生代– 新创建的对象，
旧生代 – 经过多次垃圾回收没有被回收的对象或者大对象
持久代– JVM使用的内存，包含类信息等）

==新生代采用的是复制算法，老年代采用的是标记-整理算法==

ParNew 收集器

是Serial收集器的多线程版本，除了使用多线程进行收集之外，其余的收集算法、回收策略等都是使用一样的。

用途：许多运行在server模式下的虚拟机首选的新生代收集器

特点：除Serial收集器外，目前只有它可以与CMS（第一款真正意义上的并发收集器）收集器配合工作

局限：在单个CPU中收集效果不一定比Serial好，甚至可能会由于线程间的开销，在超线程技术实现的两个CPU的环境中都不能百分百保证比Serial好。

Parallel Scavenge 收集器

是一款新生代收集器，使用复制算法并行多线程收集器。

特点：一般的收集器的关注点是在于尽可能的缩短垃圾回收时用户线程的停顿时间，而它关注的是达到一个可以控制的吞吐量。即CPU用于运行用户代码的时间和CPU总消耗时间的比值（运行用户代码的时间/（运行用户代码的时间 + 垃圾收集的时间））

Serial old 收集器

是Serial的老年代版本

特点： 单线程，使用的是标记-整理算法

用途：同样也是使用在client模式下的虚拟机使用， 如果在server模式下，JDK1.5以及之前和Parallel Scavenge收集器搭配使用，另外一种用途就是作为CMS收集器的后备预案，在并发收集器发生并行模式失败时使用。

Parallel Old 收集器

是Parallel Scavenge收集器的老年版本， 使用的是标记-整理算法

用途：主要为了配合Parallel Scavenge新生代收集器

CMS（Concurrent Mark Sweep）收集器

是一种以获得最短回收停顿时间为目标的收集器。目前很大一部分的Java应用集中在互联网站或者B/S系统的服务端，这类应用很重视服务的相应速度。

是基于标记-清除算法实现的。

1. 初始标记（需 stop the world）
   标记GC Roots能直接关联到的对象
2. 并发标记
   进行GC Roots tracing的过程
3. 重新标记（需 stop the world）
   修正并发标记期间因用户程序继续运作而导致标记产生变动的部分对象的标记记录
4. 并发清除

局限：对CPU资源敏感、无法处理浮动垃圾、由于基于标记-清除算法，会产生大量的空间碎片，会对大对象的分配带来麻烦。

G1 收集器

特点：并行与并发、分代收集（分多个大小相同的region）、空间整合（使用的是标记整理算法）

Author: Mike Xie

内存分配

在JVM中，内存是按照分代进行组织的。

垃圾回收的时候，真没有必要扫描整个堆

此处非堆内存指代的是方法区

堆内存分为年轻代和年老代，非堆内存主要是Permanent区域，主要用于存储一些类的元数据，常量池等信息。

而年轻代又分为两种，一种是Eden区域，另外一种是两个大小对等的Survivor区域。之所以将Java内存按照分代进行组织

主要是基于

1. 这样一个“弱假设-大多数对象都在年轻时候死亡。
2. 只有很少的由老对象（创建时间较长的对象）指向新生对象的引用

同时，将内存按照分代进行组织，使得我们可以在不同的分代上使用不同的垃圾回收算法，使得整个内存的垃圾回收更加有效。

对象优先在 Eden 分配

新生代

绝大多数最新被创建的对象会被分配到这里，由于大部分对象在创建后会很快变得不可到达，所以很多对象被创建在新生代，然后消失。对象从这个区域消失的过程我们称之为”minor GC“。

大对象直接进入老年代

大对象

所谓大对象是指，需要大量连续内存空间的Java对象，最典型的大对象就是那种很长的字符串以及数组大对象对虚拟机的内存分配来说就是一个坏消息，经常出现大对象容易导致内存还有不少内存空间时就不得不提前触发垃圾收集以获取足够的连续空间来“安置”它们。

老年代

对象没有变得不可达，并且从新生代中存活下来，会被拷贝到这里。其所占用的空间要比新生代多。也正由于其相对较大的空间，发生在老年代上的GC要比新生代少得多。对象从老年代中消失的过程，我们称之为”major GC“

长期存活的对象将进入老年代

虚拟机给每个对象定义了一个对象年龄计数器，如果对象在Eden出生并经历过第一次Minor GC后仍然存活，并且被Survivor容纳的话，将被移动到Survivor空间中，并且对象年龄为1.对象在Survivor区中每熬过一次Minor GC，年龄增加一岁，当它的年龄增加到一定程度(默认为15岁)，就将会被晋升到老年代中。

空间分配担保

在发生Minor GC之前，虚拟机会先检查老年代最大可用的连续空间是否大于新生代所有对象总空间，如果这个条件成立，那么Minor GC可以确保是安全的。如果不成立，则虚拟机会查看设置值是否允许担保失败。如果允许，那么会继续检查老年代最大可用的连续空间是否大于历次晋升到老年代对象的平均大小，如果大于，将尝试着进行一次Minor GC，尽管是有风险的；如果小于或者设置值不允许担保失败，则需要改为进行一次Full GC。

垃圾回收

Minor GC

1. 当Eden区满时，触发Minor GC
2. 又称新生代GC，指发生在新生代的垃圾收集动作
3. 因为Java对象大多是朝生夕灭，所以Minor GC非常频繁，一般回收速度也比较快

Full GC

1. 调用System.gc时，系统建议执行Full GC，但是不必然执行

2. 老年代空间不足

3. 方法去空间不足

4. 通过Minor GC后进入老年代的平均大小大于老年代的可用内存

5. 由Eden区、From Space区向To Space区复制时，对象大小大于To Space可用内存，则把该对象转存到老年代，且老年代的可用内存小于该对象大小

年轻代的垃圾回收

在年轻代上采用的垃圾回收算法是 “Mark-Copy” 算法，并不同于我们前面所了解的任何一种基本垃圾回收算法，但是Mark算法是一样的，基于根对象找到所有的可达对象，具体可看Mark-Sweep算法中的Mark步骤. 而对于Copy算法，它仅仅是简单的将符合一定年龄的对象从一个分代拷贝到另一个分代。

具体的回收过程如下

Author: Mike Xie

研究背景

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

/**
 *  哪个会跑的更快？
 */
public class PrimitiveVSReferenceType {
    private static final long yiyi = 100000000L; //一亿
    private static final long yiqianwan = 10000000L; //一千万

    public static void main(String[] args) {
        testPrimitiveSum(yiyi);
        testReferenceSum(yiqianwan);
    }

    public static void testPrimitiveSum(long count){
        long startTime = System.currentTimeMillis();

        long sum = 0L;
        for(int i=0; i< count;i++){  //一亿
            sum+=i;
        }

        System.out.println("testPrimitiveSum result: " + sum);
        long endTime = System.currentTimeMillis();
        System.out.println("testPrimitiveSum use time: " + (endTime - startTime));
    }

    public static void testReferenceSum(long count){
        long startTime = System.currentTimeMillis();

        Long sum = 0L;
        for(int i=0; i< count;i++){   //一千万
            sum+=i;
        }

        System.out.println("testReferenceSum result: " + sum);
        long endTime = System.currentTimeMillis();
        System.out.println("testReferenceSum use time: " + (endTime - startTime));
    }
}

java 内存模型？

java是在java虚拟机上运行，一般地大家讲到的Java内存其实就是Jvm内存

这些数据区分别有什么用？

栈区

虚拟机栈

虚拟机栈，生命周期与线程相同，是Java方法执行的内存模型。每个方法(不包含native方法)执行的同时都会创建一个栈帧结构，方法执行过程，对应着虚拟机栈的入栈到出栈的过程。

本地方法栈

本地方法栈（Native Method Stack）与虚拟机栈所发挥的作用是非常相似的，它们之间
的区别不过是虚拟机栈为虚拟机执行Java方法（也就是字节码）服务，而本地方法栈则为虚拟机使用到的Native方法服务

程序计数器

程序计数器（Program Counter Register）是一块较小的内存空间，它可以看作是当前线
程所执行的字节码的行号指示器。 在虚拟机的概念模型里（仅是概念模型，各种虚拟机可能
会通过一些更高效的方式去实现），字节码解释器工作时就是通过改变这个计数器的值来选
取下一条需要执行的字节码指令，分支、 循环、 跳转、 异常处理、 线程恢复等基础功能都需
要依赖这个计数器来完成。

堆区

对于大多数应用来说，Java堆（Java Heap）是Java虚拟机所管理的内存中最大的一块。

Java堆是被所有线程共享的一块内存区域，在虚拟机启动时创建。

此内存区域的唯一目的就是存放对象实例，几乎所有的对象实例都在这里分配内存

方法区

1. 方法区（Method Area）与Java堆一样，是各个线程共享的内存区域
2. 它用于存储已被虚拟机加载的类信息、 常量、 静态变量、 即时编译器编译后的代码等数据。
3. 虽然Java虚拟机规范把方法区描述为堆的一个逻辑部分，但是它却有一个别名叫做Non-Heap（非堆），目的应
   该是与Java堆区分开来
4. 对于习惯在HotSpot虚拟机上开发、 部署程序的开发者来说，很多人都更愿意把方法区
   称为 “永久代”（Permanent Generation），本质上两者并不等价，仅仅是因为HotSpot虚拟机的
   设计团队选择把GC分代收集扩展至方法区，或者说 使用永久代来实现方法区而已，这样
   HotSpot的垃圾收集器可以像管理Java堆一样管理这部分内存，能够省去专门为方法区编写内
   存管理代码的工作

GC 需要考虑的问题

哪些内存需要回收？

1. 线程独占区不存在垃圾回收问题：虚拟机栈、本地方法栈、程序计数器
2. 线程共享区存在垃圾回收问题： 堆区、 方法区
3. 垃圾回收的重点区域是 Java堆区，其次是方法区
4. 要回收已经死了的对象，而不是活的

如何判断对象是否已死？

引用计数法（Redis）

原理

1. 每个对象有一个引用计数器，当对象被引用一次则计数器加1，当对象引用失效一次则计数器减1，对于计数器为0的对象意味着是垃圾对象，可以被GC回收

2. 采用引用计数算法的系统只需在每个实例对象创建之初，通过计数器来记录所有的引用次数即可

例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

 public class GcDemo {

    public static void main(String[] args) {
        //分为6个步骤
        GcObject obj1 = new GcObject(); //Step 1
        GcObject obj2 = new GcObject(); //Step 2

        obj1.instance = obj2; //Step 3
        obj2.instance = obj1; //Step 4

        obj1 = null; //Step 5            = null, 去除对象引用的一种方式
        obj2 = null; //Step 6
    }
}

class GcObject{
    public Object instance = null;
}

分析

java内存模型

再回到前面代码GcDemo的main方法共分为6个步骤

1. Step1：GcObject实例1的引用计数加1，实例1的引用计数=1；
2. Step2：GcObject实例2的引用计数加1，实例2的引用计数=1；
3. Step3：GcObject实例2的引用计数再加1，实例2的引用计数=2；
4. Step4：GcObject实例1的引用计数再加1，实例1的引用计数=2；

执行到Step 4，则GcObject实例1和实例2的引用计数都等于2。

接下来继续结果图：

1. Step5：栈帧中obj1不再指向Java堆，GcObject实例1的引用计数减1，结果为1；
2. Step6：栈帧中obj2不再指向Java堆，GcObject实例2的引用计数减1，结果为1。

到此，发现GcObject实例1和实例2的计数引用都不为0，那么如果采用的引用计数算法的话，那么这两个实例所占的内存将得不到释放，这便产生了内存泄露。

存在即合理，并不能因为引用计数法不能解决对象循环应用的问题而说的引用计数法一无是处。

可达性分析法

• GC roots
• 可达性
• 基于图的深度遍历算法

依据

1. 对任何“活”的对象，一定能最终追溯到其存活在堆栈或静态存储区中的引用
2. 这个引用链条可能会穿过数个对象层次（引用传递）
3. 由此，如果从堆栈（这里指代的是运行时数据区中的栈区）或静态存储区开始，遍历所有的引用，就能找到所有的“活”的对象。
4. 对于发现每个引用，必须追踪它所引用的对象，然后是此对象包含的所有的引用
5. 如此反复进行，直到“根源于堆栈和静态存储区的引用”所形成的网络全部被访问为止。你所访问的对象都是“活”的。
6. 这个思想可以解决了“交互自引用的对象组”的问题
7. ==GC 的时候才会考虑到这些问题==

GC ROOTS

Roots tell the garbage collector where to start tracing. The garbage collector determines which blocks are reachable from the roots, and (in automatically managed pools) reclaims the unreachable blocks. This is quite efficient and can be a very good approximation to liveness.

It is therefore important that all references that the client program can directly access are registered as roots, otherwise the garbage collector might recycle an object that would be used in the future.

可作为GC roots的对象有

• 虚拟机栈中的引用对象
• 方法区中类静态属性引用的对象
• 方法区中常量引用对象
• 本地方法栈中JNI（即一般所说的Native方法）引用对象

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

 public class GcDemo {

    public static void main(String[] args) {
        //分为6个步骤
        GcObject obj1 = new GcObject(); //Step 1
        GcObject obj2 = new GcObject(); //Step 2

        obj1.instance = obj2; //Step 3
        obj2.instance = obj1; //Step 4

        obj1 = null; //Step 5
        obj2 = null; //Step 6
    }
}

class GcObject{
    public Object instance = null;
}

分析

从上图，reference1、reference2、reference3都是GC Roots，可以看出：

1. reference1-> 对象实例1；
2. reference2-> 对象实例2；
3. reference3-> 对象实例4；
4. reference3-> 对象实例4 -> 对象实例6；
5. 可以得出对象实例1、2、4、6都具有GC Roots可达性，也就是存活对象，不能被GC回收的对象。
   而对于对象实例3、5直接虽然连通，但并没有任何一个GC Roots与之相连，这便是GC Roots不可达的对象，这就是GC需要回收的垃圾对象。

结论

到这里，相信大家应该能彻底明白引用计数算法和可达性算法的 区别 吧。
再回过头来看看最前面的实例，GcObject实例1和实例2虽然从引用计数虽然都不为0，但从可达性算法来看，都是GC Roots不可达的对象。
总之，对于对象之间循环引用的情况，引用计数算法，则GC无法回收这两个对象，而可达性算法则可以正确回收。

Author: Mike Xie

垃圾收集算法

目前最基本的垃圾收集算法有四种,

1. 标记-清除算法(mark-sweep),
2. 标记-压缩算法(mark-compact),
3. 复制算法(copying)
4. 引用计数算法(reference counting).

其中标志-清除算法、标记-压缩算法、复制算法判断对象存活与否基于 可达性分析算法。

而现代流行的垃圾收集算法一般是由这四种中的其中几种算法相互组合而成，比如说，对堆(heap)的一部分采用标记-清除算法，对堆(heap)的另外一部分则采用复制算法等等

标记清除算法

基本概念

mutator && collector

collector指的就是垃圾收集器，而mutator是指除了垃圾收集器之外的部分(应用程序本身)

比如说我们应用程序本身。mutator的职责一般是NEW(分配内存),READ(从内存中读取内容),WRITE(将内容写入内存)，而collector则就是回收不再使用的内存来供mutator进行NEW操作的使用

可达性

从mutator根对象开始进行遍历，可以被访问到的对象都称为是可达对象。这些对象也是mutator(你的应用程序)正在使用的对象

原理

顾名思义，标记-清除算法分为两个阶段，标记(mark)和清除(sweep).

基于可达性分析，回头看看可达性分析存在那几个依据

标记阶段

在标记阶段，collector从mutator根对象开始进行遍历，对从mutator根对象 可以访问到的对象 都打上一个标识，一般是在对象的header中，将其记录为可达对象。

从上图我们可以看到

1. 在Mark阶段，从根对象1可以访问到B对象，从B对象又可以访问到E对象，所以B,E对象都是可达的。
2. 同理，F,G,J,K也都是可达对象。

清除阶段

collector对堆内存(heap memory)从头到尾进行线性的遍历，如果发现某个对象没有标记为可达对象-通过读取对象的header信息，则就将其回收

到了Sweep阶段，所有非可达对象都会被collector回收。

同时，Collector在进行标记和清除阶段时会将整个应用程序暂停(mutator)，等待标记清除结束后才会恢复应用程序的运行，这也是Stop-The-World这个单词的来历。

垃圾收集动作是怎么被触发的?

下面是mutator进行NEW操作的伪代码：

1
2
3
4
5
6
7
8
9
10
11
12

New():
    ref <- allocate()  //分配新的内存到ref指针
    if ref == null
       collect()  //内存不足，则触发垃圾收集
       ref <- allocate() //再次分配 (存在 OutOfMemory 的隐患，下面会分析)
       if ref == null
          throw "Out of Memory"   //垃圾收集后仍然内存不足，则抛出Out of Memory错误
          return ref

atomic collect():
    markFromRoots()
    sweep(HeapStart,HeapEnd)

标记算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

markFromRoots():
    worklist <- empty
    for each fld in Roots  //遍历所有mutator根对象
        ref <- *fld
        if ref != null && isNotMarked(ref)  //如果它是可达的而且没有被标记的，直接标记该对象并将其加到worklist中
           setMarked(ref)
           add(worklist,ref)
           mark()
mark(): 
    while not isEmpty(worklist)
          ref <- remove(worklist)  //将worklist的最后一个元素弹出，赋值给ref
          for each fld in Pointers(ref)  //遍历ref对象的所有指针域，如果其指针域(child)是可达的，直接标记其为可达对象并且将其加入worklist中
          //通过这样的方式来实现深度遍历，直到将该对象下面所有可以访问到的对象都标记为可达对象。
                child <- *fld
                if child != null && isNotMarked(child)
                   setMarked(child)
                   add(worklist,child)

在mark阶段结束后，sweep算法就比较简单了，它就是从堆内存起始位置开始，线性遍历所有对象直到堆内存末尾，如果该对象是可达对象的（在mark阶段被标记过的），那就直接去除标记位（为下一次的mark做准备），如果该对象是不可达的，直接释放内存。

1
2
3
4
5
6
7
8

sweep(start,end):
    scan <- start   //从堆内存起始位置开始
   while scan < end
       if isMarked(scan)   //如果该对象是可达对象的（在mark阶段被标记过的）
          setUnMarked(scan)   //那就直接去除标记位（为下一次的mark做准备）
      else
          free(scan)   // 如果该对象是不可达的，直接释放内存。
      scan <- nextObject(scan)

缺点

1. 效率问题： 标记 清除过程效率都不高，主要是频繁遍历堆内存
2. 空间问题： 产生大量碎片

标记-清除算法的比较大的缺点就是垃圾收集后有可能会造成大量的内存碎片，像上面的图片所示，垃圾收集后内存中存在三个内存碎片，假设一个方格代表1个单位的内存，如果有一个对象需要占用3个内存单位的话，那么就会导致Mutator一直处于暂停状态，而Collector一直在尝试进行垃圾收集，直到Out of Memory。

标记-压缩算法

前言

解决内部碎片的问题

内存碎片一直是 非移动垃圾回收器 (指在垃圾回收时不进行对象的移动)的一个问题，比如说在前面的标记-清除垃圾回收器就有这样的问题。而标记-压缩垃圾回收算法能够有效的缓解这一问题。

算法原理

标记阶段

也分为两个阶段，一个是标记(mark)，一个是压缩(compact). 其中标记阶段跟标记-清除算法中的 标记阶段是一样的

压缩阶段

它的工作就是移动所有的可达对象到堆内存的同一个区域中，使他们紧凑的排列在一起

从而将所有非可达对象释放出来的空闲内存都集中在一起，通过这样的方式来达到减少内存碎片的目的

移动对象的顺序

在压缩阶段，由于要移动 可达对象，那么需要考虑移动对象时的顺序，一般分为下面三种

1 任意顺序

即不考虑原先对象的排列顺序，也不考虑对象间的引用关系，随意的移动可达对象，这样可能会有内存访问的局部性问题。

前：

后：

2 线性顺序

在重新排列对象时，会考虑对象间的引用关系，比如A对象引用了B对象，那么就会尽可能的将A，B对象排列在一起。

3 滑动顺序

顾名思义，就是在重新排列对象时，将对象按照原先堆内存中的排列顺序滑动到堆的一端。

前：

后：

Two-Finger 算法

前言

Two-Finger算法来自Edwards, 它在压缩阶段移动对象时是任意顺序移动的

它最适用于处理包含固定大小对象的内存区域。由于Mark阶段都是跟标记-清除算法一致的，这里我们只关注Compact阶段。

原理

Two-Finger算法是一个Two Passes算法，即需要遍历堆内存两次
第一次遍历是将堆末尾的可达对象移动到堆开始的空闲内存单元去，
第二次遍历则需要修改可达对象的引用，因为一些可达对象已经被移动到别的地址，而原先引用它们的对象还指向着它们移动前的地址。

在这两次遍历过程中，首尾两个指针分别从堆的头尾两个位置向中间移动，直至两个指针相遇，由于它们的运动轨迹酷似两根手指向中间移动的轨迹，因此称为Two Finger算法。

第一次遍历

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

compact():
    relocate(HeapStart,HeapEnd) //重新定位可达对象的位置
    updateReferences(HeapStart,free) //修改可达对象的引用

relocate(start,end)
    free <- start
    scan <- end
    
    while free < scan 
        //找到一个可以被释放的空间
        while isMarked(free)
            unsetMarked(free)
            free <- free + size(free)
        
        //找到一个可以移动的可达对象
        while not isMarked(scan) && scan > free
            scan <- scan - size(scan)
            
        if scan > free
            unsetMarked(scan)
            move(scan, free) //将scan位置的可达对象移动到free位置上
            *scan <- free //将可达对象移动后的位置写到原先可达对象处于的位置
            free <- free + size(free)
            scan <- scan - size(scan)

第一次遍历的原理是

1. 头指针(free)沿着堆头向堆尾前进，直到找到一个空闲的内存单元（即没有被标记为可达对象的内存单元），如遇到可达对象，则清除其标记。
2. 接着尾指针(scan)从堆尾向堆头方向前进，直到找到一个被标记为可达的内存单元。
3. 最后，collector将可达对象从尾指针(scan)指向的位置移动到头指针(free)指向的位置，最后将可达对象移动后的位置(当前free指针指向的位置)写到原先可达对象处于的位置(当前尾指针scan指向的位置), 为下一次的遍历 - 更新对象相互间的引用做好准备。
4. 注：当移动可达对象时，其引用的对象在可达对象移动后保持不变，如下图中的G对象移动后依然指向位置5和位置10。

示例图

第二次遍历

为了更新引用关系

可见是需要STW的

目的

一个可达对象可以被其他对象引用，比如上图中的K对象，如果其被移动后，引用它的对象比如说G并不知道它被移动了，那么这第二次的遍历就是为了告诉G它所引用的对象K已经被移动到新的位置上去了，它需要更新它对K的引用。

代码

1
2
3
4
5
6
7
8
9
10
11
12

updateReferences(start,end)
    for each fld in Roots //先更新mutator根对象所引用的对象关系
        ref <- *fld
        if ref >= end
            *fld <- *ref 
    scan <- start
    while scan < ned
        for each fld in Pointers(scan)
            ref <- * fld
            if ref >= end 
                *fld <- *ref
        scan <- scan + size(scan)

分析

1. 第二次遍历，collector先会对根对象进行遍历

2. 比如根对象2引用着位置6的内存单元，根据算法，该位置大于等于end指针所指向的位置 - 即第一次遍历free指针和scan指针相遇的位置，那么我们就认为这个位置的对象已经被移动，需要更新根对象2的引用关系，即从引用位置6改为引用位置2(位置6的内存单元中记录着该对象被移动后的新位置)。

3. 同理，在移动G对象的时候，也是要判断看G所引用的内存单元位置是否大于end指针指向的位置，如果小于，则不处理。否则则修改G的引用关系。

示例图

==还有另外一种算法的==

复制算法

前言

1. 半区复制算法的目的也是为了更好的 缓解内存碎片问题。
2. 对比于标记-压缩算法, 它不需要遍历堆内存那么多次，节约了时间，但是它也带来了一个主要的缺点，那就是相比于标记-清除和标记-压缩垃圾回收器，它的可用堆内存减少了一半。
3. 同时对于大对象，复制比标记的代价更大。所以半区复制算法更一般适合回收小的，存活期短的对象。

三色抽象法

在我们深入半区复制算法原理前，我们需要了解下什么是三色抽象法。对于一个对象，垃圾收集器可以将其标记为灰色，黑色和白色中的一种，每种颜色代表不同的含义，

1. 灰色 - 表示垃圾收集器已经访问过该对象，但是还没有访问过它的所有孩子节点。
2. 黑色 - 表示该对象以及它的所有孩子节点都已经被垃圾收集器访问过了。
3. 白色 - 表示该对象从来没有被垃圾收集器访问过，这就是非可达对象。

三色抽象法也可以用在标记-清除算法和标记-压缩算法。当垃圾收集结束后，可达对象都被标记为黑色，非可达对象都被标记为白色，不会有灰色对象存在。在半区复制算法里，我们也采用了三色抽象法来标记对象。

算法原理

之所以叫半区复制，是因为它将堆内存对半分为两个半区，只用其中一个半区来进行对象内存的分配，
如果在这个半区内存不够给新的对象分配了，那么就开始进行垃圾收集，
将这个半区中的所有可达对象都拷贝到另外一个半区中去，
然后继续在另外那个半区进行新对象的内存分配。半区复制算法中比较常见是Cheney算法

代码

结合图形去分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

atomic collect():
    flip()
    scan <- free
    for each fld in Roots  //遍历处理根对象A, B
        process(fld)
    while not isEmpty(worklist)
        ref <- remove(worklist)
        scan(ref)

flip():
    fromspace, tospace <- tospace, fromspace  //交换左右半区
    top <- tospace+extent  //界定堆内存的边界
    free <- tospace

scan(ref):
    for each fld in Pointers(ref)
        process(fld)

process(fld):  //处理根对象
    fromRef <- *fld
    if fromRef != null
        *fld <- forward(fromRef) //将可达对象复制后的地址写到原对象的位置上，当作迁移地址
    
forward(fromRef):
    toRef <- forwardingAddress(fromRef) //读取该位置上对象的迁移地址
    if toRef == null //如果该位置上的对象没有迁移地址，那就说明它还没有被复制，需要复制到tospace中去
        toRef <- copy(fromRef)
    return toRef
    
copy(fromRef):
    toRef <- free 
    free <- free + size(fromRef)
    move(fromRef, toRef) //从fromRef位置复制对象到toRef位置上
    forwardingAddress(fromRef) <- toRef  //将地址toRef写到fromRef位置上的对象中去
    add(worklist, toRef)
    return toRef

remove(worklist):
    ref <- scan
    scan <- scan + size(scan)
    return ref

分析

实际上半区复制算法的实现跟标记-压缩算法的实现差不多， 都是采用的深度遍历算法，理解该算法的关键点是，

1. 怎么计算可达对象的迁移地址(forwardingAddress) - 看copy(fromRef)方法的实现，
2. 以及怎么更新对象间的引用关系 ?

我们假设A,B对象是根对象。

1. 首先先交换左右半区(ToSpace, FromSpace), 同时设置free指针和top指针。

2. 遍历处理根对象A,B。先将A对象复制到free指针指向的位置，同时将A对象复制后的地址(迁移地址)写到原先A对象所在的位置，图中虚线的箭头表示。可以看到A对象已经被collector访问过了，但是还没有访问其孩子节点，所以将其标为了灰色。紧接着scan，free指针继续向前移动。

3. 由于是深度遍历算法，紧接collector会先遍历处理A对象所引用的对象C，当发现对象C没有迁移地址时，说明它还没有被复制，由于它又是可达对象，所以接着collector会将它复制到当前free指针指向的位置，即对象A后面。对象C复制完后，会用其复制后的地址来更新A原先对C的引用，同时也写到原先C对象所在的地址上。

4. 接着collector会处理对象C的孩子节点（深度遍历算法），由于对象C没有引用任何对象，于是对象C的处理结束，将其标记为黑色。然后collector接着处理A对象的另外一个孩子节点E对象，处理方式跟处理对象C一致。

5. 对象E也没有孩子节点，collector也将其标识为黑色。

6. 到目前为此，A对象也全部处理结束了，于是collector将其标识为黑色，然后接着去处理对象B。当复制B对象结束后，发现B对象所引用的对象C有迁移地址，于是就更新其对对象C的引用，使其指向FromSpace半区中对象C的迁移地址 - 即C对象复制后所在ToSpace的地址。这个情况下就不需要再次复制对象C了。

7. 当所有的可达对象都从FromSpace半区复制到ToSpace半区后，垃圾收集结束。新对象的内存分配从free指针指向的位置开始进行分配。

引用计数算法

1. reference counting

2. 现代编程语言比如Lisp，Python，Ruby等的垃圾收集算法采用的就是引用计数算法

算法原理

通过在 对象头 中分配一个空间来保存该对象被引用的次数。如果该对象被其它对象引用，则它的引用计数加一，如果删除对该对象的引用，那么它的引用计数就减一，当该对象的引用计数为0时，那么该对象就会被回收

例子

比如说，当我们编写以下代码时，

1

String p = new String("abc")

abc这个字符串对象的引用计数值为1.（rc = reference count）

而当我们 去除 abc字符串对象的引用时，则abc字符串对象的引用计数减1

1

p = null // = null, 去除对象引用的一种方式

剖析

注意其中的对比

垃圾回收时间不一样

1. 由此可见，当对象的引用计数为0时，垃圾回收就发生了。
2. 这跟前面三种垃圾收集算法不同，前面三种垃圾收集都是在为新对象分配内存空间时由于内存空间不足而触发的

回收对象不一样

1. 前三种垃圾收集是针对整个堆中的所有对象进行的。
2. 而引用计数垃圾收集机制不一样，它只是在引用计数变化为0时即刻发生，而且只针对某一个对象以及它所依赖的其它对象。所以，我们一般也称呼引用计数垃圾收集为直接的垃圾收集机制，而前面三种都属于间接的垃圾收集机制。

而采用引用计数的垃圾收集机制跟前面三种垃圾收集机制最大的不同在于，垃圾收集的开销被分摊到整个应用程序的运行当中了，而不是在进行垃圾收集时，要挂起整个应用的运行，直到对堆中所有对象的处理都结束。因此，采用引用计数的垃圾收集不属于严格意义上的”Stop-The-World”的垃圾收集机制。这个也可以从它的伪代码实现中看出：

伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

New(): //分配内存
    ref <- allocate()
    if ref == null
        error "Out of memory"
    rc(ref) <- 0  //将ref的引用计数(reference counting)设置为0
    return ref

atomic Write(dest, ref) //更新对象的引用
    addReference(ref)
    deleteReference(dest)
    dest <- ref

addReference(ref):
    if ref != null
        rc(ref) <- rc(ref)+1
        
deleteReference(ref):
    if ref != null
        rc(ref) <- rc(ref) -1
        if rc(ref) == 0 //如果当前ref的引用计数为0，则表明其将要被回收
            for each fld in Pointers(ref)
                deleteReference(*fld)
            free(ref) //释放ref指向的内存空间

对于上面的伪代码，重点在于理解两点，

1. 第一个是当对象的引用发生变化时，比如说将对象重新赋值给新的变量等，对象的引用计数如何变化。
2. 假设我们有两个变量p和q，它们分别指向不同的对象，当我们将他们指向同一个对象时，下面的图展示了p和q变量指向的两个对象的引用计数的变化。

1
2
3

String p = new String("abc")
String q = new String("def")
p = q

当我们执行代码p=q时，实际上相当于调用了伪代码中的Write(p,q)， 即对p原先指向的对象要进行deleteReference()操作 - 引用计数减一，因为p变量不再指向该对象了，而对q原先指向的对象要进行addReference()操作 - 引用计数加一。

第二点需要理解的是，当某个对象的引用计数减为0时，collector需要递归遍历它所指向的所有域，将它所有域所指向的对象的引用计数都减一，然后才能回收当前对象。在递归过程中，引用计数为0的对象也都将被回收，比如说下图中的phone和address指向的对象。

环形数据问题

但是这种引用计数算法有一个比较大的问题，那就是它不能处理环形数据 - 即如果有两个对象相互引用，那么这两个对象就不能被回收，因为它们的引用计数始终为1。这也就是我们常说的“内存泄漏”问题。比如下图展示的将p变量赋值为null值后所出现的内存泄漏。

概念

引用计数法存在什么问题？

引用计数到底是如何维护所有对象引用的?

• 经典

Author: Yellow

关于

本文是以一种简单易懂的方式阐述Java NIO中一些基本但是可能让初学者费解的概念，参考了《进击的Java新人》和互联网上的一些资料，内容不仅限于Java，可能会牵涉到一些计算机的基础知识，比如I/O模型、操作系统知识等。

前言

当前这个时代，随着上网成本越来越低廉、终端性能越来越强大、应用种类也越来越丰富，互联网已触及我们生活中的每个角落。如今，如果一个年轻人从没点过一次美团外卖，或者从没玩过网络游戏或看过网络直播，那么他可能会被认为是刚从山洞里走出来的原始人。

而这一切便利的互联网服务的背后，是由一系列复杂的技术做支撑的，如何保证在海量用户访问的情况下服务还能稳定并且快速，这成了很多企业要着手解决的问题，毕竟谁都不想自己的产品三天两头崩溃打开一个页面要十几秒吧，如果真要那样，估计boss会提着菜刀在办公室等你了（参考J东）。

然而不管一个公司的业务是游戏，还是外卖，亦或是社交，其本质都是网络应用（包括客户端与服务器的交互、服务器与服务器的交互），所以一个公司如何想handle大量的数据、大量的用户与大量的交互，高性能网络编程必须得玩的溜。

对于大部分SSHJava程序员来说，拿SSH开发Web应用应该是家常便饭了，但如果把SSH拿掉，让他做一个网络应用（比如一个IM），他可能就懵逼了。个人认为，“框架”的确是一个好东西，特别是对于做项目、提高生产率来说；但是另一方面，如果一个程序员只是想着怎么去使用这些框架，而忽视了很多更核心更基本的东西，那对于他的个人发展来说，无异于故步自封。（见Java程序员的堕落）

另一方面，对于SSH中的核心Spring来说，其性能在不同语言的各种Web框架中也是几乎垫底的（见这个Benchmark），但是同样是基于Java的Netty却名列前茅，所以Java本身性能并不弱，弱的是Spring使用的堵塞式的I/O模型（但是最新的Spring 5似乎推出了能支持非堵塞I/O的Spring WebFlux，这个有带考察）。

所以，为了了解或者入门高性能网络编程，I/O模型的学习一定是重中之重，下面就会来谈一谈这方面的东西。（个人觉得，I/O这个东西一直都是拖累系统性能的吊车尾：内存拖累CPU、硬盘拖累内存、……，于是牛人们为了让系统不至于被拖累得那么惨，捣鼓出了各种玩意，比如Cache、LazyLoad等… 扯远了）

JavaNIO之一：传统I/O与NIO的关系

诞生历史

从Java诞生开始，伴随着JDK1.0，Java程序员们就有了相应的I/O类可以使用，比如大家熟悉的老朋友InputStream、OutputStream等等，基本都集中于java.io这个package下面。那时候用户量小，数据量小，所以大家都用得很开心。那时候的代码大概长成这个样子：

1
2

InputStream is = new FileInputStream(“a.txt”);
byte b = is.read();

到了大概两千年初，Java在其JDK1.4版本中包含了一个新的朋友：java.nio，提供了对非阻塞I/O的抽象（对下需要依赖OS的实现）。有人认为nio = Non-Blocking I/O，但是官方宣传nio = New I/O，然而是哪个并不重要，只要跟老朋友阻塞式Blocking I/O（BIO）区分开就行。

之后到了JDK1.7的时候，Java又引入了一个更新的朋友：AIO（具体的Class也是在nio package下），负责对异步I/O（Asynchronous I/O）进行抽象，然而很多OS的AIO的实现并不给力，效率不高，所以实际用处并不大。我们下面的内容主要是基于Non-Blocking I/O。

我们看到Java为我们带来了很多新朋友（Class、package），但是有一点要注意的是Java并没有创造任何I/O模型，I/O模型必须OS层面提供支持，并以syscall的形式暴露出来，Java做的工作实际上是对这些syscall的再一次封装。

有什么用处？

现代高性能服务器（Game Server、Web Server、IM Server…）、高性能通讯框架的基础，比如Netty、Nginx、Node.js、Redis、Dubbo等，虽然它们的编程语言并不相同，但是都是依赖于OS底层提供的能力实现的，最终的编程模型并不相差太多。业界经常说的C100K之类的问题，靠BIO基本是解决不了的，通常都是需要 Non-Blocking I/O（具体原因会在下面章节阐述）。所以理解这些新的I/O模型，是学习与从事高性能网络开发工作的前提。

JavaNIO之二：三大组件（Buffer、Channel、Selector）

JavaNIO基本上是围绕这3个东西进行编程：

1. Buffer：缓冲区，也就是内存中一块用来暂存数据的固定大小的区域。可以想象成一个用于装水的玻璃缸；
2. Channel：通道，数据可以通过Channel写入Buffer或从Buffer读取到别的地方，主要分为文件Channel和网络Channel两大类。可以想象下我可以用一根水管一端接水龙头，另一端伸到玻璃缸里，那么水就能源源不断地流入玻璃缸了，这根水管是一个往Buffer写数据的Channel；我还可以用另一根水管把水从玻璃缸中抽出到其它地方，这根水管是一个从Buffer读数据的Channel。
3. Selector：I/O多路复用的选择器，与Channel配合使用，是实现Non-Blocking I/O、高并发的关键，只能用于网络Channel，所以暂时先放一边，等到网络Channel时会一起讲。

所以对于前两者，它们的关系大概如下图，但是注意写入或读取的Channel都可以有多个，不仅限于一个。

JavaNIO之三：三大组件之Buffer

总体概述

学过计算机的同学应该不难理解什么是（一般意义上的）Buffer，其实JavaNIO中的Buffer类也是类似：一块尺寸在初始化之后就固定的内存区域，用来暂时存放数据。下面给出Buffer家族的类层次图：

可以看到其实Buffer是一个抽象类，在其之下是对应所有包装类型的抽象Buffer类，其实就是属性中增加了一个对应的原始数据类型的数组（比如DoubleBuffer里面比Buffer多了一个double[]）。再往下就是具体的实现类，基本上每种数据类型都至少对应两种：HeapXXXBuffer（在Java Heap中分配）和DirectXXXBuffer（在本地内存中分配），比如ByteBuffer下面的HeapByteBuffer和DirectByteBuffer。

Buffer的重要属性和操作

首先要说明的是，NIO中一些类的设计思路跟老的BIO类有些不一样，BIO虽然也可以自己new一个byte[]作为InputStream读取数据时的目的地，或OutputStream写数据时的目的地，但往往我们只需要把这个数组传进去read()或write()就行了，不需要知道读到或写到数组的什么地方，之后的工作Stream会帮我们做了。

然而NIO的使用方式相比起来却有点“原始”：管理Buffer读到哪、写到哪的工作不由Channel负责，而是回到Buffer自己身上，由程序员自己控制。最重要的属性（下标）有3个：

1. position：指向当前可被操作的位置（操作为读or写）
2. limit：指向可被操作的边界（如果是写操作，则表示空闲位置的边界；如果是读操作，则表示有效数据的边界）
3. capacity：Buffer的Size，Buffer被初始化之后就是一个固定值

它们的大小关系是：position <= limit <= capacity。只看文字有点抽象难理解，下面会结合图示说明。为了方便理解，你可以认为Buffer具有两种模式：读数据时处于读模式，写数据是处于写模式。然而实际上Buffer并没有这两种模式的设置，只是你可以逻辑上这样认为。

1.初始化

一个刚刚初始化好的空的Buffer（可以理解成做好准备可以写数据了！）长这样：

mark是什么可以先不管。capacity就是初始化时设定的Buffer的Size，这里是10。position指向的是当前可以被操作的位置，因为我们现在是写模式，所以它指向的是当前可以写的一个空位。limit则指向可写的边界，可以理解成写到哪就不允许继续往下写了，因为我们这是刚刚创建的空Buffer，默认下可以写到全部满位置，所以这时候limit = capacity = 10。

2.顺序写入几个字符

假设我们现在依次往Buffer里面写入5个字符 H、 e、 l、 l 、o：

1

buffer.put((byte)'H').put((byte)'e').put((byte)'l').put((byte)'l').put((byte)'o');

则每写入一个字符，position都会向右移一个位置，写了5个字符后，它就指向5这个位置。现在它看起来像这样：

3.随机写入

假设我们要直接修改Buffer中的某个位置，可以这样做：

1

buffer.put(0, (byte)'M');

这样做会把原先位置0的字符‘H’修改为‘M’，并且随机写入不会改变position的位置（它还是指向5）。如果这时候我们再顺序写入一个字符‘w’，这个字符是会写在位置5的，现在它看起来像这样：

1

buffer.put((byte)'w');

4.翻转！变成读模式

PS：flip操作经常会让刚接触NIO的人费解！所以下面内容请仔细阅读！

假设现在我们要读出Buffer里的数据，直接调用get()是不行的，因为读操作也要依赖position、limit，而这时候position是指向一个空位置，所以读不出先前写进Buffer里的数据。于是这时候我们需要一个翻转操作：

1

buffer.flip();

flip()执行后产生如下效果：

1. 当前limit变成先前position的值；
2. 当前position变成0。
   
   可以简单理解成Buffer变成了读模式，position指向了当前可以被读的字符，limit则指向字符串的尾巴（也就是最多允许读到哪里为止）。之后就可以调用get()来读取数据了，每次读position都会往右移动一个位置，直到limit为止。

总结

上面罗列了Buffer的3个重要属性和flip操作，其中理解flip操作非常关键。可以想想，如果我们连续调用两次flip()，会产生什么效果？答案就是这个Buffer变成既不能读也不能写了，因为position、limit都指向0了。

Heap Buffer与Direct Buffer

一般我们new出来的Buffer都是在Java Heap中分配的空间，在里面的空间可以被GC回收，但有时候我们为了性能考虑，比如不想GC干扰或增加GC压力，可以考虑在Java进程中的Native内存中分配Buffer，这时候的Buffer称为Direct Buffer，可以通过allocateDirect(int capacity)获得。但是分配在Native内存中的Buffer不能被GC回收，所以如果要使用，请参考这里：Deallocating Direct Buffer Native Memory in Java for JOGL

Heap Buffer与Direct Buffer在Java进程中的布局图如下所示：

JavaNIO之四：三大组件之Channel

Channel可以想象成一个管子，一头连接着I/O数据来源/目的地（文件、网络等），一头连接着Buffer，数据可以在这两者之间传输。

Channel按照面向的设备的不同，可以分为两种：

1. FileChannel（面向磁盘文件）
2. SocketChannel、ServerSocketChannel（面向网络数据流）

SocketChannel、ServerSocketChannel将在之后跟着Selector一起讲，这里先讲FileChannel。另外从JDK1.7开始多了一些以Asynchronous打头从Channel类，这是属于AIO部分的东西，这里也不作阐述。

如何使用

可以通过FileChannel类的open()函数方便地创建一个与某个文件关联的FileChannel对象。常用的API大概有下面这些：

1
2
3
4
5
6
7

public abstract int read (ByteBuffer dst, long position)
public abstract int write (ByteBuffer src, long position)
public abstract long size()
public abstract long position()
public abstract void position (long newPosition)
public abstract void truncate (long size)
public abstract void force (boolean metaData)

用起来跟Stream类差不多，特别注意的是force()这个函数，它可以强制OS把数据刷写到磁盘上，因为有时候我们对FileChannel进行写入时，数据不一定已经落到磁盘上，可能在OS的cache中。

内存映射文件（Memory Mapped File）

如果不提及内存映射文件，那么NIO中的FileChannel用起来其实跟BIO的Stream差不多。然而这个特性是NIO开始引入的（底层还是依赖OS的支持），能在一些场景下提供非常好的性能，所以应该重点关注。

虚存空间（Virtual Address Space）

要讲清楚什么是内存映射文件，必须先弄明白什么是虚存空间（以下简称VAS）。VAS可以理解成进程运行的“沙箱”，每一个进程都运行在一个单独的VAS里，在32bit的机器上，这个VAS大小为4GB。那是不是表示如果运行了10个进程，就需要占用10 x 4GB = 40GB的内存呢？显然不是的，其实VAS只是一个虚拟概念，只是从进程角度看，它觉得自己拥有一个4GB这么大的内存空间，它可以load一段数据并放在地址0x12345678这个位置，然而在真正的物理内存这边，数据并不一定是放在这个地址，虚存地址和物理内存地址之间需要靠一个叫内存管理单元（MMU）的硬件做转换。可以参考下面图示，如果还是不懂，可以自行Google。

这样做好处主要是可以隔离不同的进程，防止恶意进程对其它进程进行破坏。

另外一方面，4GB的虚拟空间进一步可以分成2部分：内核空间和用户空间。CPU也有两种运行状态：内核态和用户态。内核空间里一般放驱动、硬件缓冲区等敏感信息，不能随意读写，而用户空间则存放一般经常分配的内存空间。CPU在用户态时，可以访问用户空间，但不能访问内核空间和执行里面的代码；CPU变成内核态后，可以访问内核空间和读写硬件。用户态到内核态之间的转换一般通过中断或系统调用（system call）。

BIO vs. Memory Mapped File

现在可以来解释内存映射文件了。首先我们来看老的BIO读文件时，数据是怎样在设备和内存中跑的：

假设一个文件在Disk中，大小是3个块，现在进程想读取文件的第一个块。

1. 首先，进程发起一个系统调用，这时候CPU变成内核态；
2. CPU在内核空间开辟一块缓冲区，并命令Disk把数据装载到这个内核缓冲区中，这时候进程需要堵塞等待硬件完成这个数据装载；
3. 数据装载到内核缓冲区结束，进程把数据从内核缓冲区Copy到用户空间。

从这个步骤可以看出，数据经历了2次Copy：Disk -> 内核空间，内核空间 -> 用户空间。写数据到Disk的时候流程也是类似，可以看出在数据量大的情况下，这种方式比较低效。

在支持内存映射文件的OS上，可以绕过内核空间，直接把整个文件“投影”到用户空间，这个“投影”操作时很快的，然而这时候它并不真正的Copy数据到用户空间，只是对于进程来说“看起来像是”整个文件都在内存中了。当进程需要文件的第一块数据时，会产生一个Page Fault，OS会自动从Disk帮忙把第一块数据加载到用户空间中；类似的，写数据只需要写入用户空间，而不需要堵塞，OS会帮忙同步回Disk中。图示：

这项特性主要应用场景有：高性能文件随机读写、高性能进程间通信（不同编程语言也可以）

Java API

FileChannel类中有一个map()函数：

1

public abstract MappedByteBuffer map(MapMode mode, long position, long size)

MappedByteBuffer是一个抽象类，从JDK1.8代码上看只有一个实现类DirectByteBuffer，它是上面我们讲过的在Native空间分配的Direct Buffer。例子代码可以在自行Google。

JavaNIO之五：三大组件之Selector

由于Selector只跟网络的Channel有关，所以它们放到这里一起讲。

堵塞式I/O的年代

回忆下以前学Java Socket编程时一个最简单的服务器-客户端例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

public class Server {
    public static void main(String args[]) throws IOException{
        ServerSocket ss = new ServerSocket(8080);
        Socket conn = ss.accept();  // 堵塞！
        BufferedReader br = new BufferedReader(new InputStreamReader(conn.getInputStream()));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(conn.getOutputStream()));
        String s = br.readLine();  // 堵塞！
        while (s != null) {
            System.out.println(s);
            bw.write(s.toUpperCase() + "\n");  // 堵塞！
            bw.flush();
            s = br.readLine();  // 堵塞！
        }

        br.close();
        bw.close();
        conn.close();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

public class Client {
    public static void main(String args[]) throws IOException {
        Socket conn = new Socket("127.0.0.1", 8080);  // 堵塞！
        BufferedReader br = new BufferedReader(new InputStreamReader(conn.getInputStream()));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(conn.getOutputStream()));
        bw.write("hello\n");  // 堵塞！
        bw.flush();
        String s = br.readLine();  // 堵塞！
        System.out.println(s);

        bw.write("world\n");  // 堵塞！
        bw.flush();
        s = br.readLine();  // 堵塞！
        System.out.println(s);


        br.close();
        bw.close();
        conn.close();
    }
}

这是个很简单的例子，先运行服务器，进程会堵塞在ss.accept();这个地方，然后再运行客户端，它们会建立链接。之后客户端会发送“hello”和“world”两个字符串给服务器，服务器收到后打印出来，之后就退出。实际上上述代码注释里标注了“堵塞！”的地方都会产生堵塞，因为都牵涉到网络I/O，线程必须等待数据准备好了（已经从网卡读入到内核缓冲区了，或者已经从用户空间写入内核缓冲区了，参考上面章节的文件I/O），才能继续运行。

从这个例子可以看出一个问题：当服务器线程正在为一个客户端服务时，是不能服务其它客户端的，如果要同时服务多个客户端，就需要启动多个服务器线程/进程，这就是老的一些http服务器使用的模型。然而这会带来一些问题：

1. CPU个数是非常有限的，启动的线程很多的话，势必会频繁地切换，产生非常严重的上下午切换开销；
2. 每个线程为了维护一些栈之类的只跟自身相关的信息，也需要占用一定的内存，那么线程一多势必占用大量内存。

加上互联网应用大部分都是一些“慢连接”式的请求，往往大部分时间都在等待数据，只有很少部分时间会传输一点数据（比如在线聊天、网页消息推送…），用堵塞式I/O来处理这些请求，往往到“千”级别的并发就遇到瓶颈了。

不同的网络I/O模型

由于传统的模型行不通了，就需要寻求新的出路。著名的《APUE》里总结了几种网络I/O模型，这里结合一个生活中的例子：学生做试卷。一堆学生在教室里做试卷，假设不规定交卷试卷，学生做完就可以交卷，老师必须拿到试卷回到办公室才能批改。

1. 同步 + 堵塞式I/O模型

所谓同步，即表示把数据从内核空间Copy到用户空间的过程必须线程自己负责；所谓堵塞，表示发起系统调用之后进程要block住一直等到数据准备就绪。用学生做试卷的例子来说就是，如果只有1位老师，那么这位老师就要站在某个学生旁边一直盯着他做试卷，直到他做完后，亲手把试卷拿回办公室，期间其余同学如果有做完想交卷都是不行的，因为老师只能盯着一开始那位学生。如果想做到每个学生都能自由交卷，就必须每个学生配备一个老师，这堆老师都站在教室里各盯着一个学生做试卷……傻不傻？

2. 同步 + 非堵塞式I/O模型

相比之前的模型，现在发起系统调用之后不用block住了，而是可以马上返回，去做其它事情，之后周期性地检查数据是不是准备好，准备好了就拷贝数据到用户空间。这种模型往往跟“I/O多路复用”结合，即一个线程可以monitor多个网络socket。用学生做试卷的例子来说就是，老师把试卷派下去之后，就回办公室玩手机了，而办公室有一个装置，当有任何学生做完试卷了，就会让这个装置发生变化（比如亮灯），老师打完一盘王者荣耀了，抬起头看看装置亮灯了，就走过去教室把做好的试卷收过来。这样一个老师就可以服务多个学生了。

3. 纯异步式I/O模型

相比之前的模型，这个模型连从内核空间拷贝数据到用户空间都不需要线程自己做了，线程发起请求后留下一个回调接口就可以了，等数据准备好之后就会调用该回调接口。用学生做试卷的例子来说就是，老师派完试卷后就回办公室了，学生做完试卷后自己把试卷拿到办公室给老师。是不是很完美？然而真正OS实现上现在AIO还不成熟，效率甚至还不如NIO。

I/O多路复用（Multiplexing）

I/O多路复用一般是指结合 同步 + 非堵塞式I/O模型，用一个线程监视大量socket的技术，当有socket变成Ready了，这个线程就能获知。一般Linux底层提供的有poll/select、epoll几种技术，poll/select差不多，都是线程只能获知有socket ready了，但是不知道是哪些socket，所以必须要一个个socket去check；而epoll则连哪些socket变成ready了也能获知，所以性能更高。

Selector API

JavaNIO中与I/O多路复用有关的3大类：

1. SelectableChannel（Socket & ServerSocket），代表socket
2. Selector，监听器，可以监听多个socket
3. SelectionKey，抽象表示一个Selector与一个channel的监听关系
   SelectableChannel与Selector是多对多关系：
   

用法参考下面API或自行Google：

1
2
3
4
5
6
7
8
9

//SelectableChannel（Socket类）
public abstract SelectionKey register (Selector sel, int ops)
//Selector
public abstract int select (long timeout)
//SelectionKey
public final boolean isReadable()
public final boolean isWritable()
public final boolean isConnectable()
public final boolean isAcceptable()

Author: Jonas Yu

目录

• Socket介绍
• 基于Socket的Java网络编程
• 分层网络协议

Socket介绍

网络上两个程序通过一个双向的通讯链接实现数据交换，这个双向链路的一端称为一个Socket。Socket通常用来实现客户端和服务器端的通信,在Internet上的主机一般会运行多个服务软件，软件一旦需要跟互联网上其他计算机之间通信，就需要通过Socket来绑定到一个端口，这个端口则是计算机用来标识对应的Socket进行数据传递。一个Socket由一个IP地址和一个端口唯一确定。

基于Socket的Java网络编程

基于TCP通讯过程：
通常情况下，服务端的Socket会监听某个端口是否有连接请求，当服务端接收到客户端的连接请求时，会向客户端发送接收的消息，这样一个连接就建立了。客户端与服务端都可以通过Socket进行数据通信。

Java的网络编程的接口大多数位于 java.net 和 java.nio 这两个package里，掌握这两个package是Java程序员必备的基础技能。Java.net中提供了两个类Socket和ServerSocket，分别用来表示双向连接的客户端和服务端。

下面是使用Socket跟ServerSocket来实现简单的C/S程序代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

public class Server {
    public static void main(String args[]) throws IOException, InterruptedException {
        ServerSocket ss = new ServerSocket(8000);
        System.out.println("Accept start *** ");
        Socket conn = ss.accept();
        System.out.println("Accept in progress ");
        BufferedReader br = new BufferedReader(new InputStreamReader(conn.getInputStream()));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(conn.getOutputStream()));
        String s = br.readLine();
        while (s != null) {
            System.out.println("Receive: " + s);
            Thread.sleep(5000);
            bw.write(s.toUpperCase() + "\n");
            bw.flush();
            System.out.println("Send: " + s.toUpperCase());
            s = br.readLine();
        }

        br.close();
        bw.close();
        conn.close();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

public class Client {
    public static void main(String args[]) throws IOException, InterruptedException {
        Socket conn = new Socket("127.0.0.1", 8000);
        BufferedReader br = new BufferedReader(new InputStreamReader(conn.getInputStream()));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(conn.getOutputStream()));
        System.out.println("conn server success !");
        Thread.sleep(2000);
        bw.write("hello\n");
        bw.flush();
        System.out.println("hello has been send.");
        String s = br.readLine();
        System.out.println(s);
        Thread.sleep(5000);
        bw.write("world\n");
        bw.flush();
        System.out.println("world has been send.");
        s = br.readLine();
        System.out.println(s);
        br.close();
        bw.close();
        conn.close();
    }
}

从上面代码可以看出，Socket通信步骤如下:

1. 服务端通过指定端口号实例化ServerSockt对象，调用accept函数阻塞等待连接请求
2. 客户端通过IP跟端口实例化Socket对象
3. 客户端跟服务端分别得到一个Socket对象，根据Socket对象，得到对应的输出流跟输入流，通过这两个IO可以进行两个端之间的通信

分层网络协议

OSI模型
OSI模型是国际标准化组织ISO创立的。这是一个理论模型，并无实际产品完全符合OSI模型。制订OSI模型只是为了分析网络通讯方便而引进的一套理论。也为以后制订实用协议或产品打下基础。OSI模型共分七层：从上至下依次是

• 应用层 指网络操作系统和具体的应用程序，对应WWW服务器、FTP服务器等应用软件
• 表示层：数据语法的转换、数据的传送等
• 会话层：建立起两端之间的会话关系，并负责数据的传送
• 传输层：负责错误的检查与修复，以确保传送的质量，是TCP工作的地方。
• 网络层：提供了编址方案,IP协议工作的地方(数据包）
• 数据链路层：将由物理层传来的未经处理的位数据包装成数据帧
• 物理层：对应网线、网卡、接口等物理设备(位)

TCP/IP四层模型
在实际开发中，我们不会使用这种模型，更常用的是TCP/IP协议族的四层模型。
这四层模型分别对应的是：

• 应用层 最上面一层是应用层，负责处理特定的应用程序消息。例如Telnet，Ftp, Http等。

• 传输层 主要为两台主机上的应用程序提供端到端的通信。在 TCP/IP 协议族中，有两种传输协议：TCP（传输控制协议）和UDP（用户数据报协议） 。TCP为两台主机提供高可靠性的数据通信。它所做的工作包括把应用程序交给它的数据分成合适的小块交给下面的网络层，确认接收到的分组，设置发送最后确认分组的超时时钟等。由于运输层提供了高可靠性的端到端的通信，因此应用层可以忽略所有这些细节。另一种传输协议，UDP则为应用层提供一种非常简单的服务。它只是把称作数据报的分组从一台主机发送到另一台主机，但并不保证该数据报能到达另一端。任何必需的可靠性必须由应用层来提供。这两种运输层协议分别在不同的应用程序中有不同的用途。

• 网络层 处理分组在网络中的活动，例如分组的选路。在TCP/IP协议族中，网络层协议包括 IP 协议（网际协议） ，ICMP 协议（Internet互联网控制报文协议） ，以及 IGMP 协议（Internet组管理协议） 。

• 链路层 也称作数据链路层，通常包括操作系统中的设备驱动程序和计算机中对应的网络接口卡。它们一起处理与电缆（或其他任何传输媒介）的物理接口细节。这一层大约相当于OSI模型中的物理层和链路层的总和。

OSI分层模型和TCP/IP分层模型的对应关系：

Author: Kelvin

注意： 由于红黑树删除相对复杂，看到另一篇博客写的非常好，故本文内容基本来自红黑树删除，代码自己实现)

一、节点命名约定

 D表示要被删除的节点。即：取 Delete 的首字母
 P 表示父节点。即：取 Parent 的首字母
 S表示兄弟姐妹节点。即：取  Sibling的首字母
 U表示叔伯节点。即：取Uncle的首字母
 G表示祖父节点。即：取  Grandfather的首字母
 L表示左树。即：取Left的首字母
 R表示右树。即：取Right的首字母
 Nil表示叶子节点。即所谓的空节点；注意：红黑树中的叶子节点与其他树中所述说的叶子节点不是同一概念。而且红黑树中的叶子节点(即：Nil节点)永远是被定义为黑色的

下文的节点命名表示将会使用以上这些命名约定或它们的组合表示。因此，请先牢记这些命名约定。举例
DR表示要被删除的节点的右子树，即：右子节点；
SL表示兄弟节点的左子树，即：左子节点；
…

二、删除操作宏观分析

在红黑树中，删除一个节点往大的说，只有以下四种情况。

情况一：删除的节点的左、右子树都非空；
情况二：删除的节点的左子树为空树，右子树非空；
情况三：删除的节点的右子树为空树，左子树非空；
情况四：删除的节点的左、右子树都为空树；

其中情况一，可以按与其他二叉搜索树的删除方式一样处理，最终可以转换到后面的三种情况。具体为：找到(Old)D节点的直接后继节点(暂且称为X节点)，然后将X的值转移到D节点，最后将X节点作为真正要被删除掉的节点(即：(Real)D节点)。这样删除操作后，可以保证该树仍然为一棵二叉搜索树。但由于红黑树的定义(即：红黑树的性质)约定。这样删除(Real)D节点后，可能会破坏红黑树的性质。所以需要额外做一些调整处理，这便是下面将要详细讨论的内容。

说明：下文中所提到的D，除非有特别说明，否则都将指的是(Real)D。

三、红黑树删除后平衡处理

在具体分析之前，再次列出红黑树的定义：
  (1) 每个节点或者是红色，或者是黑色
  (2) 根节点一定是黑色
  (3) 所有叶子节点都是黑色的。【红黑树中的叶子节点也叫NIL节点，是指空的叶子节点】
  (4) 如果一个节点是红色的，则它的子节点必须是黑色的。（任何两个父子节点不可能同时为红色）
  (5) 任意节点到其所有分支叶子节点的简单路径上的黑色节点个数相同。（该属性保证红黑树始终是一颗接近平衡的二叉树）
下面是几个图示说明：

根据红黑树的定义，被删除的节点D(即：上文所述的(Real)D节点)不论如何都一定有一个“右子树”，只是该右子树要不为非空树(即：真正存在的节点，不为Nil节点)，要不就必为空树(即：D的两个子节点都为Nil)。下面称D的该右子节点(或称为右子树)为DR。

a) 被删除的D节点为红色。这种情况，则与D相关的颜色以及结构关系必然只有如下一种情况(为什么只有这种情况，不明白的请看红黑树的性质)：
分析：因为D为红色，所以P必为黑色，同时DR不可能为红色(否则违反性质4)。同时由于性质5，则DR必为Nil，否则就D树来说，经过DR与不经过DR的路径的黑节点数必不相同。现在要删除D节点，只需要直接将D节点删除，并将DR作为P的左子节点即可。因此删除后，变成上图右侧所示。

b) 被删除的D节点为黑色。此时情况会稍复杂些，具体又分析为：DR为Nil与DR不为Nil。根据性质5，如果DR不为Nil，则DR必为红色，且DR的两个子节点必为Nil。因此，此处先来分析DR不为Nil的情况(因为该情况比较简单)。而DR为Nil的情况，由后面的C)及其后内容再进行具体分析 。
如前所述，如果DR不为Nil，则D、DR必为如下情况：
分析：由于删除的D为黑色，删除后P的左子树的黑节点数必少1，此时刚好DR为黑色，并且删除后DR可以占据D的位置(这样仍是一棵二叉搜索树，只是暂时还不是合格的红黑树罢了)，然后再将DR的颜色改为黑色，刚好可以填补P左子树所减少的黑节点数。从而P树又平衡了。因此，平衡处理后，最终变成上图右侧的图示。

c) 被删除的D为黑色，且DR为Nil。
如果DR为Nil，则删除D后，P的左子树黑节点数必定少1，纯粹想在P的左子树做文章来平衡P树是绝无可能的了。因此，必定需要其他分支的辅助来最终完成平衡调整。根据红黑树的定义，P会有一个右子节点，称为S子节点。此处又可细节分两种情况：黑S与红S。此处先讨论红S的情况。

说明：如果S为黑，则它必不会为Nil。(不明白的人，再好好想想为什么)。同时根据红黑树的性质，D、S、P、SL、SL的颜色关系必只有如下一种情况(因为此处探讨的是S为红的情况)。

分析：删除前P树的左、右子树的黑节点数平衡，删除后(即：上图右侧所示)，经过DR分支的黑节点数将比通过S分支的黑节点数少1。此时，做如下操作
将P左旋转，再将P由黑色改为红色，将S由红色改为黑色，演变过程如下图示：

经过以上演变后，经过P的路径，左分支黑节点数仍是少1，其他分支的黑节点数做仍然保持不变。此时的情况却变成DR的兄弟节点为黑色(不再是红色的情况了)，因此转入此处c)点一开始所说的另一种情况(S为黑色的情况)的处理。

注意：可能有人会一时想不明白什么要这样转换。因为这样转换后，虽然对于P树的左子树的黑节点数仍然会比右子树的黑节点数少1，但此时DR的兄弟(以前的S节点)现在已经变为SL，即已经由红色变为黑色，并且非常重要的此时的DR的兄弟节点SL的子结点(即：DR的两个侄子节点)，要不就是红色节点要不就必为Nil节点，而这种情况正是D为黑色、S也黑色的情况。(注意看注意看注意看一定注意看这点：对于被删除节点D的父节点来说，D黑S黑的情况下，无论如何D的兄弟节点S的两个儿子节点SL与SR都不可能是非Nil的黑节点。不明白的好好想想为什么)。因此我们有了进一步分析的余地。

d) 被删除的D为黑色，S也为黑色的情况。根据D、P、S、SL、SR的颜色组合情况，本来是有非常多种变换的。但事实上，我们只需要按如下4种情况做进一步的处理，即可全部涵盖所有的颜色组合情况。
d.1> SL为红，SR颜色任意；(对于该情况的处理，其实我们不关心P的颜色)
d.2> SR为红，SL颜色任意；(对于该情况的处理，其实我们不关心P的颜色)
d.3> SL、SR都为黑；P为红。(注意：根据前面c)点的红色文字部分的分析，此时SL与SR必定必定都为Nil节点)；
d.4> SL、SR都为黑；P为黑。(注意：根据前面c)点的红色文字部分的分析，此时SL与SR必定必定都为Nil节点)；

d.1> SL为红，SR颜色任意情况

分析：P树的左子树黑节点数减少1，因此，要想平衡，必需想办法让左子树的黑结节数增加1，而且同时P的右子树的黑节点数要保持不变。因此，想办法将SL这个红色节点利用起来，让它来填补P的左子树所缺少的黑节点个数。因此，立马想到旋转，只要有办法转到P的左子树或P位置上，则就有可能填平P左子树的高度。所以具体操作步骤为：
将S右旋转；接着将SL改为P的颜色，P的颜色改为黑色(用这个黑色来填补DR分支的黑节点数)；将P左旋转。

d.2> SR为红色，SL颜色任意的情况

分析：思路同d.1>情况类似，都是想办法用红色的SR节点来填补P的左子树的减少的黑节点数。具体步骤为：
将S由黑色改为P的颜色；
将SR由红色改为黑色；
将P的颜色改为黑色(用该黑色来填补DR分支缺失的黑节点数)；
将P节点左旋转；

d.3> SL、SR都为黑色(其实都为Nil节点)，P为红色的情况

分析：此情况较为简单，直接将红色的P改为黑色，以此为填补DR缺少的黑节点个数。此时P右子树黑节点数却增多，因此，再将S改为红色即可平衡。

d.4> SL、SR都为黑色(其实都为Nil节点)，P为黑色的情况

分析：因为DR、P、S、SL、SR全都为黑色，则不论如何变换，都永远不可能使用P的左右子树的黑节点数达到平衡。而P不平衡的原因是因为P的右子树黑节点数会比左子树多1个。因此，干脆将S由黑色改为红色，如此一来，P的左、右子树的黑节点个数是平衡的。但是，此时经过P的路径的黑节点个数将会比不经过它的路径少一个。因此，我们将P作为待平衡的节点(即：此时的P相当于DR的角色)往上继续上溯，直到P为根节点为止。

四、红黑树删除代码实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150

//删除节点
	public void remove(T key){
		RBTNode<T> node = search(this.mRoot, key);
		if(null!=node){
			remove(node);
		}
	}
	
	private void remove(RBTNode<T> node) {
		RBTNode<T> child=null,parent=null;
		boolean color=false;
		
		//删除的节点有两个孩子,转化为删除该节点的后继节点
		if((node.left!=null) && (node.right!=null)){
			//记录后继节点
			RBTNode<T> replace = node.right;
			while(replace.left!=null)
				replace = replace.left;
			
			child = replace.right;
			parent = replace.parent;
			if(parent==node){
				node.right = child;
				if(child!=null){
					child.parent = node;
				}
			}else {
				parent.left = child;
				if(child!=null){
					child.parent = parent;
				}
			}
				
			//将后继节点数据拷贝到待删除节点
			node.key = replace.key;	
			color = replace.color;
			if(color==BLACK){
				removeFixUp(child,parent);
			}
			replace = null;
			return;
		}
		
		if(node.left!=null){
			child = node.left;
		}else {
			child = node.right;
		}
		parent = node.parent;
		
		if(parent!=null){
			if(parent.left==node){
				parent.left = child;
			}else {
				parent.right = child;
			}
		}else {
			this.mRoot = child;
		}
		
		if(child!=null){
			child.parent = parent;
		}
		if(node.color==BLACK){
			removeFixUp(child,parent);
		}
		node = null;
	}

	//删除节点后，修正红黑树
	private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
		//node的兄弟节点
		RBTNode<T> silNode = null;
		
		//如果node是黑色的话，那么必为NIL节点
		while((node == null || isBlack(node)) && (node != this.mRoot)){
			if (parent.left == node) {
				silNode = parent.right;
				if(isRed(silNode)){		//case 1: 兄弟节点是红色节点，则parent为黑色，silNode的两个儿子都为黑色
					setBlack(silNode);
					setRed(parent );
					leftRotate(parent);
					silNode = parent.right;
				}

				//case 2: 兄弟节点是黑色节点,其左右孩子都为黑色
				if((silNode.left==null || isBlack(silNode.left) && (silNode.right==null || isBlack(silNode.right)))){
					setRed(silNode);
					node = parent;
					parent = parentOf(node);
					continue;
				}else {
					//case 3: 兄弟节点是黑色，左孩子是红色，右孩子是黑色
					if(silNode.right==null || isBlack(silNode.right)){
						if(silNode.left!=null)
							setBlack(silNode.left);
						setRed(silNode);
						rightRotate(silNode);
						silNode = parent.right;
					}

					//case 4: 兄弟节点黑色，左孩子任意颜色，右孩子是红色
					silNode.color = parent.color;
					setBlack(parent);
					if(silNode.right!=null){
						setBlack(silNode.right);
					}
					leftRotate(parent);
					break;
				}
			}else {
				silNode = parent.left;
				if(isRed(silNode)){
					setBlack(silNode);
					setRed(parent );
					rightRotate(parent);
					silNode = parent.left;
				}

				if((silNode.left==null || isBlack(silNode.left) && (silNode.right==null || isBlack(silNode.right)))){
					setRed(silNode);
					node = parent;
					parent = parentOf(node);
					continue;
				}else {
					//case 3: 兄弟节点是黑色，左孩子是黑色，右孩子是红色
					if(silNode.left==null || isBlack(silNode.left)){
						if(silNode.right!=null)
							setBlack(silNode.right);
						setRed(silNode);
						leftRotate(silNode);
						silNode = parent.left;
					}

					//case 4: 兄弟节点黑色，右孩子任意颜色，左孩子是红色
					silNode.color = parent.color;
					setBlack(parent);
					if(silNode.left!=null){
						setBlack(silNode.left);
					}
					rightRotate(parent);
					break;
				}
			}
		}
		
		//如果node不是NIL节点，则必为红色
		if(node != null)
			setBlack(node);
	}

了解红黑树及所有代码实现，请看另一篇博客 红黑树

Author: Kelvin

一、红黑树介绍

  红黑树(Red-Black Tree, 简称RBTee)，是一种特殊的二叉查找树。它满足二叉查找树的特征： 任意一个节点所包含的键值，大于左孩子的键值，小于等于右孩子的键值。
  顾名思义，红黑树的每个节点上具有一个表示颜色的属性，红色或者黑色。

• 红黑树的节点定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

public class RBTNode<T extends Comparable<T>> {
	boolean color;
	T key;
	RBTNode<T> left;
	RBTNode<T> right;
	RBTNode<T> parent;
	
	public RBTNode(boolean color, T key) {
		this.color = color;
		this.key = key;
	}

	public RBTNode(boolean color, T key, RBTNode<T> left, RBTNode<T> right,
			RBTNode<T> parent) {
		super();
		this.color = color;
		this.key = key;
		this.left = left;
		this.right = right;
		this.parent = parent;
	}
	
}

• 红黑树的特征
  必须满足以下特征的二叉查找树才是红黑树。
    (1) 每个节点或者是红色，或者是黑色
    (2) 根节点一定是黑色
    (3) 所有叶子节点都是黑色的。【红黑树中的叶子节点也叫NIL节点，是指空的叶子节点】
    (4) 如果一个节点是红色的，则它的子节点必须是黑色的。（任何两个父子节点不可能同时为红色）
    (5) 任意节点到其所有分支叶子节点的简单路径上的黑色节点个数相同。（该属性保证红黑树始终是一颗接近平衡的二叉树）

二、红黑树的基本操作（左旋和右旋）

• 左旋
  
  代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

/* 
	 * 对红黑树的节点(x)进行左旋转
	 * 左旋示意图(对节点x进行左旋)：
	 *      px                           px
	 *     /                            /
	 *    x                            y                
	 *   / \      --(左旋)-.          / \       
	 *  lx  y                        x  ry     
	 *     / \                      / \
	 *    ly ry                    lx ly  
	 */
	public void leftRotate(RBTNode<T> p){
		RBTNode<T> parent = p.parent;	// 父节点
		RBTNode<T> pRightSon = p.right; //右孩子
		RBTNode<T> pRrigtGrandLeftSon = pRightSon.left;//右孩子的左孩子
		
		pRightSon.parent = parent;
		if(parent != null){
			if(p == parent.left){
				parent.left = pRightSon;
			}else if(p == parent.right){
				parent.right = pRightSon;
			}
		}else {
			this.mRoot = pRightSon;
		}
		
		pRightSon.left = p;
		p.parent = pRightSon;
		
		p.right = pRrigtGrandLeftSon;
		if(pRrigtGrandLeftSon != null){
			pRrigtGrandLeftSon.parent = p;
		}
	}

• 右旋
  
  代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/* 
	 * 对红黑树的节点(y)进行右旋转
	 *
	 * 右旋示意图(对节点y进行右旋)：
	 *            py                             py
	 *           /                              /
	 *          y                              x                  
	 *         /  \      --(右旋)-.            /  \                     
	 *        x   ry                         lx  y  
	 *       / \                                / \                   
	 *      lx  rx                             rx  ry
	 * 
	 */
	public void rightRotate(RBTNode<T> p){
		RBTNode<T> parent = p.parent;	//父节点
		RBTNode<T> pLeftSon = p.left;	// 左节点
		RBTNode<T> pleftGrandRightSon = pLeftSon.right; // 左孙，即左节点的右节点
		
		pLeftSon.parent = parent;
		if(parent != null){ //判断旋转的节点是否有父节点
			if(p == parent.left){
				parent.left = pLeftSon;
			}else if(p == parent.right){
				parent.right = pLeftSon;
			}
		}else {
			this.mRoot = pLeftSon;
		}
		
		pLeftSon.right = p;
		p.parent = pLeftSon;
		
		p.left = pleftGrandRightSon;
		if(pleftGrandRightSon != null){
			pleftGrandRightSon.parent = p;
		}
	}

三、添加节点

我们知道，一棵树之所以成为红黑树，必须要满足红黑树的五个特征。对红黑树的插入操作，必然有可能会影响红黑树特性，因此我们需要对其进行修正。红黑树的插入主要分为三个步骤：
  1. 将红黑树当作一颗二叉查找树，将节点插入
  2.将插入的节点着色为”红色”
  3.通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。

• 插入节点后，对红黑树的影响分析
  新插入的节点，默认是红色（因为如果是黑色，就会直接影响红黑树的特性5，调整很麻烦）；我们设置新插入的节点为N，其父节点为P，其祖父节点为G，其父亲P的兄弟节点为U。当父节点P是黑色的，不需要调整，下面主要讨论P是红色的情况。

1. 当U是红色的。将P和U重绘为黑色并重绘结点G为红色。现在新结点N有 了一个黑色的父结点P，因为通过父结点P或叔父结点U的任何路径都必定通过祖父结点G， 在这些路径上的黑结点数目没有改变。但是，红色的祖父结点G的父结点也有可能是红色 的，这就违反了性质3。为了解决这个问题，我们在祖父结点G递归向上调整颜色
   
2. 当U是黑色，且N是左孩子。对祖父结点G 的一次右旋转; 在旋转产生的树中，以前的父结点P现在是新结点N和以前的祖父节点 G 的父结点，然后交换以前的父结点P和祖父结点G的颜色，结果仍满足红黑树性质
   
3. 当U时黑色，且N是右孩子。我们对P进行一次左旋转调换新结点和其父 结点的角色，就把问题转化成了第二种情况，此时对G做一次有旋转即可。
   
   
   以上所分析的是当P是左孩子时的情况，当P时右孩子的情况跟是左孩子的情况一样，旋转的方向不一样而已，请读者自行分析。

• 红黑树的插入代码实现

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119

  //添加节点 public void insert(T key){ if(null==key){ return; } this.insert(new RBTNode<T>(BLACK, key)); } private void insert(RBTNode<T> node){ if(this.mRoot==null){ this.mRoot = node; return; } RBTNode<T> curr = this.mRoot; int rs = 0; while(true){ rs = node.key.compareTo(curr.key); if(rs < 0){ if(curr.left != null){ curr = curr.left; }else { curr.left = node; node.parent = curr; break; } }else { if(curr.right != null){ curr = curr.right; }else { curr.right = node; node.parent = curr; break; } } } node.color = RED; //由于新插入节点会影响红黑树的结构，需要修正使其满足红黑树的性质 insertFixUp(node); } //插入节点后修正红黑树 private void insertFixUp(RBTNode<T> node) { RBTNode<T> parent, gparent; parent = parentOf(node); //若父节点存在，且父节点的颜色是红色 while((parent = parentOf(node))!=null && isRed(parent)){ gparent = parentOf(parent); if(gparent==null){ break; } //若父节点是祖父节点的左孩子 if(parent == gparent.left){ //叔叔节点 RBTNode<T> uncle = gparent.right; // case 1: 叔叔节点是红色 if(uncle!=null && isRed(uncle)){ setBlack(uncle); setBlack(parent); if(gparent != this.mRoot){ setRed(gparent); } node = gparent; continue; } //case 2: 叔叔是黑色，当前节点是右孩子或者叔叔是null else if(parent.right==node){ leftRotate(parent); setBlack(node); if(gparent != this.mRoot){ setRed(gparent); } rightRotate(gparent); node = parent; } //case 3: 叔叔是黑色，当前节点是左孩子或者叔叔是null else{ setBlack(parent); if(gparent != this.mRoot){ setRed(gparent); } rightRotate(gparent); } }else { //父节点是祖父节点的右孩子 RBTNode<T> uncle = gparent.left; // case 4: 叔叔节点是红色 if(uncle!=null && isRed(uncle)){ setBlack(uncle); setBlack(parent); if(gparent != this.mRoot){ setRed(gparent); } node = gparent; continue; } //case 5:叔叔节点是黑色，且当前节点是左孩子或者叔叔是null else if(parent.left == node){ rightRotate(parent); setBlack(node); if(gparent != this.mRoot){ setRed(gparent); } leftRotate(gparent); node = parent; } else {//case 6:叔叔节点是黑色，且当前节点是右孩子或者叔叔是null setBlack(parent); if(gparent != this.mRoot){ setRed(gparent); } leftRotate(gparent); } } } }

四、删除节点

由于红黑树的删除较复杂，请看另一篇博客 红黑树的删除

五、红黑树代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487

package cn.kelvin.oocl.rbtree;

import java.util.ArrayDeque;
import java.util.Queue;

public class RBTree<T extends Comparable<T>> {
	RBTNode<T> mRoot;
	private static final boolean RED   = false;
    private static final boolean BLACK = true;
    
    public RBTree() {
	}
    
    public RBTree(T rootKey) {
    	this.mRoot = new RBTNode<T>(BLACK, rootKey);
   	}
	
    //添加节点
	public void insert(T key){
		if(null==key){
			return;
		}
		this.insert(new RBTNode<T>(BLACK, key));
	}
	
	private void insert(RBTNode<T> node){
		if(this.mRoot==null){
			this.mRoot = node;
			return;
		}
		RBTNode<T> curr = this.mRoot;
		int rs = 0;
		while(true){
			rs = node.key.compareTo(curr.key);
			if(rs < 0){
				if(curr.left != null){
					curr = curr.left;
				}else {
					curr.left = node;
					node.parent = curr;
					break;
				}
			}else {
				if(curr.right != null){
					curr = curr.right;
				}else {
					curr.right = node;
					node.parent = curr;
					break;
				}
			}
		}
		node.color = RED;
		
		//由于新插入节点会影响红黑树的结构，需要修正使其满足红黑树的性质
		insertFixUp(node);
	}
	
	//插入节点后修正红黑树
	private void insertFixUp(RBTNode<T> node) {
		RBTNode<T> parent, gparent;
		parent = parentOf(node);
		//若父节点存在，且父节点的颜色是红色
		while((parent = parentOf(node))!=null && isRed(parent)){
			gparent = parentOf(parent);
			if(gparent==null){
				break;
			}
			
			//若父节点是祖父节点的左孩子
			if(parent == gparent.left){
				//叔叔节点
				RBTNode<T> uncle = gparent.right;
				
				// case 1: 叔叔节点是红色
				if(uncle!=null && isRed(uncle)){
					setBlack(uncle);
					setBlack(parent);
					if(gparent != this.mRoot){
						setRed(gparent);
					}
					node = gparent;
					continue;
				}
				//case 2: 叔叔是黑色，当前节点是右孩子或者叔叔是null
				else if(parent.right==node){
					leftRotate(parent);
					setBlack(node);
					if(gparent != this.mRoot){
						setRed(gparent);
					}
					rightRotate(gparent);
					node = parent;
				}
				//case 3: 叔叔是黑色，当前节点是左孩子或者叔叔是null
				else{
					setBlack(parent);
					if(gparent != this.mRoot){
						setRed(gparent);
					}
					rightRotate(gparent);
				}
			}else { //父节点是祖父节点的右孩子
				RBTNode<T> uncle = gparent.left;
				// case 4: 叔叔节点是红色
				if(uncle!=null && isRed(uncle)){
					setBlack(uncle);
					setBlack(parent);
					if(gparent != this.mRoot){
						setRed(gparent);
					}
					node = gparent;
					continue;
				}
				
				//case 5:叔叔节点是黑色，且当前节点是左孩子或者叔叔是null
				else if(parent.left == node){
					rightRotate(parent);
					setBlack(node);
					if(gparent != this.mRoot){
						setRed(gparent);
					}
					leftRotate(gparent);
					node = parent;
				}
				else {//case 6:叔叔节点是黑色，且当前节点是右孩子或者叔叔是null
					setBlack(parent);
					if(gparent != this.mRoot){
						setRed(gparent);
					}
					leftRotate(gparent);
				}
			}
			
		}
	}

	//删除节点
	public void remove(T key){
		RBTNode<T> node = search(this.mRoot, key);
		if(null!=node){
			remove(node);
		}
	}
	
	private void remove(RBTNode<T> node) {
		RBTNode<T> child=null,parent=null;
		boolean color=false;
		
		//删除的节点有两个孩子,转化为删除该节点的后继节点
		if((node.left!=null) && (node.right!=null)){
			//记录后继节点
			RBTNode<T> replace = node.right;
			while(replace.left!=null)
				replace = replace.left;
			
			child = replace.right;
			parent = replace.parent;
			if(parent==node){
				node.right = child;
				if(child!=null){
					child.parent = node;
				}
			}else {
				parent.left = child;
				if(child!=null){
					child.parent = parent;
				}
			}
				
			//将后继节点数据拷贝到待删除节点
			node.key = replace.key;	
			color = replace.color;
			if(color==BLACK){
				removeFixUp(child,parent);
			}
			replace = null;
			return;
		}
		
		if(node.left!=null){
			child = node.left;
		}else {
			child = node.right;
		}
		parent = node.parent;
		
		if(parent!=null){
			if(parent.left==node){
				parent.left = child;
			}else {
				parent.right = child;
			}
		}else {
			this.mRoot = child;
		}
		
		if(child!=null){
			child.parent = parent;
		}
		if(node.color==BLACK){
			removeFixUp(child,parent);
		}
		node = null;
	}

	//删除节点后，修正红黑树
	private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
		//node的兄弟节点
		RBTNode<T> silNode = null;
		
		//如果node是黑色的话，那么必为NIL节点
		while((node == null || isBlack(node)) && (node != this.mRoot)){
			if (parent.left == node) {
				silNode = parent.right;
				if(isRed(silNode)){		//case 1: 兄弟节点是红色节点，则parent为黑色，silNode的两个儿子都为黑色
					setBlack(silNode);
					setRed(parent );
					leftRotate(parent);
					silNode = parent.right;
				}

				//case 2: 兄弟节点是黑色节点,其左右孩子都为黑色
				if((silNode.left==null || isBlack(silNode.left) && (silNode.right==null || isBlack(silNode.right)))){
					setRed(silNode);
					node = parent;
					parent = parentOf(node);
					continue;
				}else {
					//case 3: 兄弟节点是黑色，左孩子是红色，右孩子是黑色
					if(silNode.right==null || isBlack(silNode.right)){
						if(silNode.left!=null)
							setBlack(silNode.left);
						setRed(silNode);
						rightRotate(silNode);
						silNode = parent.right;
					}

					//case 4: 兄弟节点黑色，左孩子任意颜色，右孩子是红色
					silNode.color = parent.color;
					setBlack(parent);
					if(silNode.right!=null){
						setBlack(silNode.right);
					}
					leftRotate(parent);
					break;
				}
			}else {
				silNode = parent.left;
				if(isRed(silNode)){
					setBlack(silNode);
					setRed(parent );
					rightRotate(parent);
					silNode = parent.left;
				}

				if((silNode.left==null || isBlack(silNode.left) && (silNode.right==null || isBlack(silNode.right)))){
					setRed(silNode);
					node = parent;
					parent = parentOf(node);
					continue;
				}else {
					//case 3: 兄弟节点是黑色，左孩子是黑色，右孩子是红色
					if(silNode.left==null || isBlack(silNode.left)){
						if(silNode.right!=null)
							setBlack(silNode.right);
						setRed(silNode);
						leftRotate(silNode);
						silNode = parent.left;
					}

					//case 4: 兄弟节点黑色，右孩子任意颜色，左孩子是红色
					silNode.color = parent.color;
					setBlack(parent);
					if(silNode.left!=null){
						setBlack(silNode.left);
					}
					rightRotate(parent);
					break;
				}
			}
		}
		
		//如果node不是NIL节点，则必为红色
		if(node != null)
			setBlack(node);
	}

	private void setRed(RBTNode<T> node) {
		if(node != null)
			node.color = RED;
	}

	private void setBlack(RBTNode<T> node) {
		if(node != null)
			node.color = BLACK;
	}

	private boolean isRed(RBTNode<T> node) {
		return ((node!=null) && (node.color==RED)) ? true : false;
	}
	
	private boolean isBlack(RBTNode<T> node) {
		return ((node!=null) && (node.color==BLACK)) ? true : false;
	}

	private RBTNode<T> parentOf(RBTNode<T> node) {
		return (node!=null) ? node.parent : null;
	}

	/* 
	 * 对红黑树的节点(x)进行左旋转
	 * 左旋示意图(对节点x进行左旋)：
	 *      px                           px
	 *     /                            /
	 *    x                            y                
	 *   / \      --(左旋)-.           / \                #
	 *  lx  y                        x  ry     
	 *     / \                      / \
	 *    ly ry                    lx ly  
	 */
	public void leftRotate(RBTNode<T> p){
		RBTNode<T> parent = p.parent;	// 父节点
		RBTNode<T> pRightSon = p.right; //右孩子
		RBTNode<T> pRrigtGrandLeftSon = pRightSon.left;//右孩子的左孩子
		
		pRightSon.parent = parent;
		if(parent != null){
			if(p == parent.left){
				parent.left = pRightSon;
			}else if(p == parent.right){
				parent.right = pRightSon;
			}
		}else {
			this.mRoot = pRightSon;
		}
		
		pRightSon.left = p;
		p.parent = pRightSon;
		
		p.right = pRrigtGrandLeftSon;
		if(pRrigtGrandLeftSon != null){
			pRrigtGrandLeftSon.parent = p;
		}
	}
	
	/* 
	 * 对红黑树的节点(y)进行右旋转
	 *
	 * 右旋示意图(对节点y进行右旋)：
	 *            py                             py
	 *           /                              /
	 *          y                              x                  
	 *         /  \      --(右旋)-.            /  \
	 *        x   ry                         lx  y  
	 *       / \                                / \
	 *      lx  rx                             rx  ry
	 * 
	 */
	public void rightRotate(RBTNode<T> p){
		RBTNode<T> parent = p.parent;	//父节点
		RBTNode<T> pLeftSon = p.left;	// 左节点
		RBTNode<T> pleftGrandRightSon = pLeftSon.right; // 左孙，即左节点的右节点
		
		pLeftSon.parent = parent;
		if(parent != null){ //判断旋转的节点是否有父节点
			if(p == parent.left){
				parent.left = pLeftSon;
			}else if(p == parent.right){
				parent.right = pLeftSon;
			}
		}else {
			this.mRoot = pLeftSon;
		}
		
		pLeftSon.right = p;
		p.parent = pLeftSon;
		
		p.left = pleftGrandRightSon;
		if(pleftGrandRightSon != null){
			pleftGrandRightSon.parent = p;
		}
	}
	
	//查找节点
	public RBTNode<T> search(RBTNode<T> root,T key){
		if(null==root || null==key){
			return null;
		}
		int cmp = key.compareTo(root.key);
		if(cmp<0)
			return search(root.left, key);
		else if(cmp>0)
			return search(root.right, key);
		else 
			return root;
	}
	
	public void inOrder(RBTNode<T> root){
		if(root!=null){
			inOrder(root.left);
			System.out.print(root.key.toString()+ " ");
			inOrder(root.right);
		}
	}
	
	public void preOrder(RBTNode<T> root){
		if(root!=null){
			System.out.print(root.key.toString()+ " ");
			preOrder(root.left);
			preOrder(root.right);
		}
	}
	
	public void postOrder(RBTNode<T> root){
		if(root!=null){
			postOrder(root.left);
			postOrder(root.right);
			System.out.print(root.key.toString()+ " ");
		}
	}
	
	/**
	 * 层次遍历
	 * @param root
	 */
	public void listOrder(RBTNode<T> root){
		if(root==null){
			return;
		}
		Queue<RBTNode<T>> queue = new ArrayDeque<>();
		queue.offer(root);
		RBTNode<T> curr = null;
		while(!queue.isEmpty()){
			curr = queue.poll();
			System.out.print(curr.key.toString()+" ");
			if(curr.left != null){
				queue.offer(curr.left);
			}
			if(curr.right != null){
				queue.offer(curr.right);
			}
		}
	}
	public void listOrderWithColor(RBTNode<T> root){
		if(root==null){
			return;
		}
		Queue<RBTNode<T>> queue = new ArrayDeque<>();
		queue.offer(root);
		RBTNode<T> curr = null;
		while(!queue.isEmpty()){
			curr = queue.poll();
			System.out.print(curr.key.toString()+"->"+(curr.color ? "B":"R")+" ");
			if(curr.left != null){
				queue.offer(curr.left);
			}
			if(curr.right != null){
				queue.offer(curr.right);
			}
		}
	}
	
	public class RBTNode<T extends Comparable<T>> {
		boolean color;
		T key;
		RBTNode<T> left;
		RBTNode<T> right;
		RBTNode<T> parent;
		
		public RBTNode(boolean color, T key) {
			this.color = color;
			this.key = key;
		}

		public RBTNode(boolean color, T key, RBTNode<T> left, RBTNode<T> right,
				RBTNode<T> parent) {
			super();
			this.color = color;
			this.key = key;
			this.left = left;
			this.right = right;
			this.parent = parent;
		}
		
	}
}

Author: Mike

树的基本概念

基本概念

1
2
3
4
5
6
7
8
9
10

树的度—— 一棵树中最大的结点度数 
双亲—— 孩子结点的上层结点叫该结点的双亲
兄弟—— 同一双亲的孩子之间互成为兄弟 
祖先—— 结点的祖先是从根到该结点所经分支上的所有结点
子孙—— 以某结点为根的子树中的任一结点都成为该结点的子孙
结点的层次—— 从根结点算起，根为第一层，它的孩子为第二层……
堂兄弟—— 其双亲在同一层的结点互称为堂兄弟。
深度—— 树中结点的最大层次数
有序树—— 如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。
森林—— m(m0)棵互不相交的树的集合

形象表示

m叉树定义

每个结点的度数 <= m;

二叉树

于是二叉树有如下五种形态

二叉树的子树有左右之分，不能颠倒

特殊的二叉树

满二叉树

重点是 满
形象表示（图片中数字仅代表编号，不代表真实数值）

1.定义： 高度为h，并且含有(2^h)-1个结点的二叉树
2.对于编号为 i 的结点，如果有双亲，双亲为 i/2 向下取整；如果有左孩子，左孩子编号为 2i，如果有右孩子，右孩子编号为 (2i + 1)

完全二叉树

1.若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
2.如果有度为 1 的结点，那只可能有一个，且该节点只有左孩子，而无右孩子

满二叉树、完全二叉树、非完全二叉树对比

二叉排序树

形象表示

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

定义

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则 左子树 上所有结点的值均 <= 它的 根结点 的值；
（2）若右子树不空，则 右子树 上所有结点的值均 >= 它的 根结点 的值；
（3）左、右子树也分别为二叉排序树 (递归定义)；

平衡二叉树

形象表示

定义

平衡二叉树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的 左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，同时，平衡二叉树必定是二叉搜索树，反之则不一定

二叉树性质

性质1 在二叉树的第 i 层上至多有 2^(i-1)个 结点(i>=1)

用数学归纳法证明：
归纳基础：i=1时，有2^(i-1)=2^0=1。因为第1层上只有一个根结点，所以命题成立。
归纳假设：假设对所有的 j ( 1<=j < i ) 命题成立，即第j层上至多有 2^(j-1) 个结点，证明j=i时命题亦成立。
归纳步骤：根据归纳假设，第 i-1 层上至多有2^(i-2)个结点。由于二叉树的每个结点至多有两个孩子，故第 i 层上的结点数至多是第 i-1 层上的最大结点数的2倍。即 j=i 时，该层上至多有2×2^(i-2)=2^(i-1)个结点，故命题成立。

性质2 深度为k的二叉树至多有2^k-1个结点(k≥1)。

至多，即视之为满二叉树
证明：计算等比数列 2^0+2^1+…+2^(k-1)=2^k-1

性质3 在任意-棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则no=n2+1。

回顾 m叉树 的性质

1. 设m叉树中，度数为 i 的结点树为 Ni, 则总结点数为： N = N0 + N1 + … + Nm;
2. N = 分支数 + 1 , 1 为根结点
3. 于是 N = N0 + N1 + …+ Nm = 0(N0) + 1(N1) + … + m*(Nm) + 1
4. 对应于现在所讨论的二叉树，于是有 N = N0 + N1 + N2 = N1 + 2*(N2) + 1，于是等到结论 N0 = N2 + 1

详细证明

证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)应等于0度结点数、1度结点(记为n1)和2度结点数之和：
n=no+n1+n2 (式子1)
　 另一方面，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：
nl+2n2
　　树中只有根结点不是任何结点的孩子，故二叉树中的结点总数又可表示为：
n=n1+2n2+1 (式子2)
　　由式子1和式子2得到：
no=n2+1

二叉树遍历

二叉树的前中后序的遍历，坐标名词针对的是 根节点；无论何种遍历，左孩子永远比右孩子前

• 先序递归遍历 先访问根结点，再前序遍历左子树，最后前序遍历右子树。可见，这个操作的定义就是递归的

  1 2 3 4 5 6 7 8

  public void pre_order_traversal_recursion_way(Node root) { if (root == null) { return; } out.print(root.data + " "); pre_order_traversal_recursion_way(root.left); pre_order_traversal_recursion_way(root.right); }

• 中序递归遍历 先中序遍历左子树，再访问根结点，最后中序遍历右子树。由于左子树上的值都比根结点小，右子树上的值都比根结点大，所以，中序遍历一棵树所得到的结果，是从小到大有序的，可以根据这个特点，来检验你的中序遍历是否正确实现了

  1 2 3 4 5 6 7 8

  void mid_order_traversal_recursion_way(Node root){ if(root == null){ return; } mid_order_traversal_recursion_way(root.left); out.print(root.data+" "); mid_order_traversal_recursion_way(root.right); }

• 后序递归遍历 先后序遍历左子树，再后序遍历右子树，最后访问根结点

  1 2 3 4 5 6 7 8

  void post_order_traversal_recursion_way(Node root){ if(root == null){ return; } post_order_traversal_recursion_way(root.left); post_order_traversal_recursion_way(root.right); out.print(root.data+" "); }

• 非递归先序遍历 先让根节点进栈，只要栈不为空，就可以做弹出操作；每次弹出一个结点，记得把它的左右结点都进栈。记得先右孩子，这样可以保证右子树在栈中总处于左孩子树的下面。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  void pre_order_traversal_not_recursion_way(Node root) throws StackEmptyException { Stack<Node> stack = new Stack(100); Node currentNode= root; stack.push(currentNode); while (!stack.isEmpty()){ currentNode = stack.pop(); out.print(currentNode.data + " "); if(currentNode.right != null){ stack.push(currentNode.right); } if(currentNode.left != null){ stack.push(currentNode.left); } } }

• 非递归中序遍历

一直遍历到左子树最下边，边遍历边保存根节点到栈中
当p为空时，说明已经到达左子树最下边，这时需要出栈了
进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)

1
2
3
4
5
6
7
8
9
10
11
12
13
14

private void mid_order_traversal_not_recursion_way(Node root) throws StackEmptyException {
        Stack<Node> stack = new Stack(100);
        Node currentNode = root;
        while (currentNode != null || !stack.isEmpty()){
            if(currentNode != null){
                stack.push(currentNode);
                currentNode = currentNode.left;
            }else{
                Node topNode = stack.pop();
                out.print(topNode.data + " ");
                currentNode = topNode.right;
            }
        }
    }

• 层次遍历 队列，先进先出；每出一个结点，其左右孩子进队；依此类推

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  private void level_order(Node root){ Queue<Node> queue = new LinkedList(); Node currentNode = root; queue.add(currentNode); while (!queue.isEmpty()){ currentNode = queue.poll(); out.print(currentNode.data+ " "); if(currentNode.left != null){ queue.add(currentNode.left); } if(currentNode.right != null){ queue.add(currentNode.right); } } }

数学归纳法：

1）当n=1时,显然成立.
2）假设当n=k时（把式中n换成k,写出来）成立,
则当n=k+1时,（这步比较困难,化简步骤往往繁琐)该式也成立.
由（1）（2）得,原命题对任意正整数均成立